Сотрудники Лаборатории теоретической физики ОИЯИ вывели наиболее общие формулы, которые позволяют получать многопетлевые ренормгрупповые уравнения в произвольном обобщении Стандартной модели (СМ) без необходимости явного расчета миллионов диаграмм Фейнмана, возникающих в старших порядках теории возмущения.
Рис. 1. Стандартная модель
Благодаря работе БАК мы знаем, что Стандартная модель элементарных частиц прекрасно описывает огромное количество процессов на масштабах энергий, доступных современным ускорителям. В Стандартной модели имеется восемнадцать параметров, описывающих взаимодействия фермионов (кварков и лептонов), векторных (фотон, W/Z-бозоны) и скалярных (хиггс) бозонов. Например, среди них — «константа» сильного взаимодействия, определяющая эффективную силу взаимодействия кварков и антикварков. Или хорошо известная электромагнитная константа, связанная с электрическим зарядом. Задав их, или, лучше сказать, измерив, можно делать предсказания.
Однако ученые уже много лет ищут сигналы новой физики за пределами Стандартной модели. Теоретики пытаются построить обобщения CМ, а экспериментаторы стремятся найти следы новых частиц и выявить новые взаимодействия.
Если вы расширяете СМ, то добавляете новые параметры. Например, можно предположить существование более тяжелого аналога Z-бозона, взаимодействие которого с другими частицами задается новой калибровочной «константой» (обычно обозначаются как g). Или добавить несколько бозонов Хиггса, взаимодействие которых друг с другом, а также с кварками и лептонами будет задаваться «константами» самодействия (L) и Юкавскими «константами» (y) соответственно.
«Часто важно понять, что происходит с моделью, если попытаться экстраполировать ее в область больших энергий, не доступных современным (и, возможно, даже будущим) ускорителям. Или, наоборот, задав модель Новой физики на очень высоком масштабе энергий (обычно предполагается, что в этом случае модель обладает большей симметрией, чем СМ), интересно понять, какие отклонения от предсказаний СМ можно измерить в экспериментах», — рассказал Александр Бедняков, начальник сектора квантовой теории поля ЛТФ ОИЯИ, один из авторов работы.
«Ренормгрупповые уравнения показывают, как благодаря рождению виртуальных частиц происходит экранировка или антиэкранировка зарядов при изменении энергетического масштаба (ᵣ). Такого рода эффекты имеют универсальную природу, и мы пытаемся учитывать их в наших расчетах. Каждая новая петля соответствует рождению и поглощению какой-то виртуальной частицы. Чем сложнее модель, тем мы больше имеем различных вариантов», — пояснил Александр. Он добавил, что для того, чтобы найти зависимость «зарядов» от масштаба в конкретной модели, необходимо проводить трудоемкие вычисления диаграмм Фейнмана.
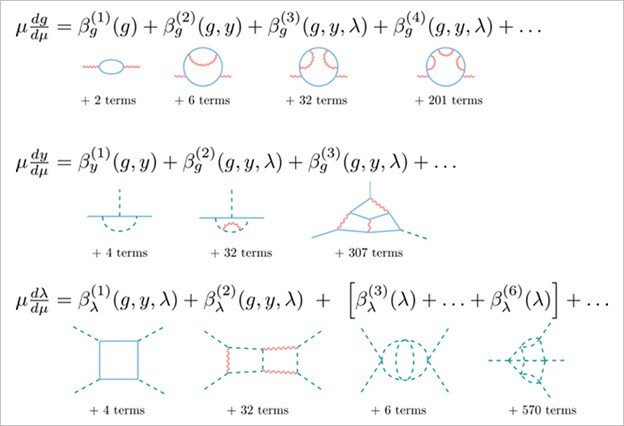
Выполненные в ходе работы сложные вычисления были преобразованы в формулы, представляющие собой достаточно простые дифференциальные уравнения. Задав значения параметров (силу взаимодействия) на одном масштабе, можно найти их значения на другом масштабе. На рис. 2 схематично показаны полученные в цикле работ наиболее общие ренормгрупповые уравнения для калибровочных, юкавский «констант», а также для самодействия скалярных бозонов. Видно, что число слагаемых в формулах растет вместе с порядком теории возмущений. Каждое слагаемое можно представить в виде диаграммы Фейнмана, где сплошные линии соответствуют фермионам, волнистые — калибровочным бозонам, а пунктирные — скалярным частицам.
Готовые уравнения удобны тем, что все расчеты сложных интегралов, соответствующих диаграммам, уже проведены. Достаточно лишь задать модель, т.е. перечислить все частицы и выписать лагранжиан — функцию, описывающую их квантовые числа и взаимодействия.
Эти уравнения могут также применяться неспециалистами в петлевых вычислениях: например, их могут использовать физики-теоретики для анализа Новой физики. Также эти готовые формулы находят свое применение в физике конденсированного состояния – в теории фазовых переходов второго рода для расчета различных критических индексов. Этот результат был отмечен как один из самых ярких, полученных ЛТФ ОИЯИ в 2021 году. Авторы цикла работ, посвященных этой тематике, Александр Бедняков и Андрей Пикельнер, были удостоены первой Премии ОИЯИ за 2021 год в категории «За научно-исследовательские теоретические работы».
Рис. 2. Общие ренормгрупповые уравнения для калибровочных, юкавский «констант» и для самодействия скалярных бозонов
«Другой важный результат цикла тесно связан с квантовой хромодинамикой (КХД), описывающей кварки, глюоны и их взаимодействия. Мы верим, что квантовая хромодинамика должна работать как при больших, так и при малых энергиях», — продолжил Александр. На больших расстояниях взаимодействие между кварками становится настолько сильным, что использование стандартной теории возмущений затруднено. На помощь приходят компьютерные вычисления на дискретной евклидовой пространственно-временной решетке. Такими расчетами занимается, в частности, коллаборация High Precision QCD (Quantum chromodynamics), в которую входят физики-теоретики научных центров Америки, Англии, Италии, Японии, Испании. Среди всего прочего они извлекают из решеточных данных ключевые параметры КХД — массы кварков и постоянную сильного взаимодействия.
«Можно взять массу кварка или константу сильного взаимодействия, измеренные при высоких энергиях, и сравнить ее с тем, что извлекают на решетке. Если сходится – это означает, что квантовая хромодинамика «работает». Если не сходится – возникает вопрос: надо ли модифицировать модель или всего лишь улучшить точность теоретических расчетов. Часто именно высокая точность позволяет найти небольшие отклонения — возможные признаки Новой физики», — прокомментировал исследователь. Важным нюансом здесь является то, что ту величину, которую извлекают из решеточных данных, часто нельзя непосредственно сравнивать с аналогичной, но используемой в физике высоких энергий. «Этот произвол "заложен" в теорию перенормировок, но мы можем его контролировать в рамках теории возмущений. Именно такого рода пересчетные формулы и были найдены нами в трехпетлевом приближении. Нам очень приятно, что наши расчеты были незамедлительно использованы коллаборацией HPQCD для нового рекорда точности в определении массы очарованного кварка», — подытожил Александр Бедняков.
Ключевые результаты работ представляют сами ученые.
Новая эра ренормгрупповых вычислений в ЛТФ: современные методы, инструменты и последние достижения
Метод ренормализационной группы (РГ) позволяет систематически улучшать точность расчетов в теории возмущений. Ключевую роль в нем играют ренормгрупповые функции, задающие отклик различных величин на изменение масштаба. Их расчет является отдельной задачей и представляет собой одну из наиболее трудоемких и технически сложных частей РГ анализа.
В представленном цикле работ обсуждаются различные аспекты многопетлевых расчетов, а также последние достижения, связанные с обобщением недавних рекордных вычислений в СМ и φ4 на случай произвольных кванто-полевых моделей.
В рамках наиболее общей перенормируемой теории в четырех измерениях впервые были выведены формулы для бета-функций калибровочных и юкавских констант взаимодействия в четырех и трех петлях соответственно [1]. Оригинальность используемого подхода состоит в том, что рассматривались простые игрушечные теории и с их помощью фиксировались модельно независимые коэффициенты в выражениях для РГ функций, минуя трудоемкие и громоздкие вычисления. Благодаря нашим расчетам стало возможно провести РГ анализ произвольной модели Новой физики на новом уровне точности без необходимости явного диаграммного счета и процедуры перенормировки. В качестве приложения найденных формул нами были выведены четырехпетлевые бета-функции всех калибровочных констант в СМ, а также в ее обобщении с несколькими хиггсовскими дублетами. Кроме того, впервые были получены шестипетлевые выражения для РГ функций как безразмерных, так и размерных параметров наиболее общего варианта теории φ4 [2]. Одним из возможных применений этого результата является изучение классов универсальности в теории критического поведения, соответствующих различным симметриям и различным параметрам порядка.
Важным шагом на пути к указанным результатам являются расчеты в рамках конкретных физических моделей. В частности, существенное влияние на дальнейшие исследования оказало вычисление четырехпетлевых электрослабых вкладов в бета-функцию сильной константы связи в СМ [3]. Благодаря тщательному анализу неопределенностей, возникающих при наивном подходе к размерной регуляризации киральных теорий, был получен ответ, подтвержденный впоследствии независимым вычислением и обобщенный в дальнейшем на случай произвольной теории поля [Poole&Thomsen (2019)]. Также был рассмотрен скалярный сектор простейшего расширения СМ с дополнительным хиггсовским дублетом [4] и найдены соответствующие РГ функции на уровне трех петель. Одним из побочных результатов расчета оказалось исправление опечаток в работах 80-х годов, повсеместно используемых в компьютерных кодах для анализа Новой физики.
Другим приоритетным результатом является вывод трехпетлевых формул, позволяющих связать непертурбативные расчеты на решетке с ключевыми параметрами КХД (сильной константой связи [5] и массами кварков [6]), используемыми при вычислении наблюдаемых в коллайдерных экспериментах. Для этих целей впервые с помощью оригинальных идей было проведено трудоемкое аналитическое вычисление трехпетлевых вершинных функций [7] в симметричной кинематике. Актуальность расчета подтверждается тем, что полученный результат [6] был немедленно использован коллаборацией HPQCD для улучшения точности решеточного вычисления массы очарованного кварка.
Современные расчеты в старших порядках возмущения немыслимы без автоматизации и применения новых подходов и алгоритмов для вычисления диаграмм Фейнмана. В работах цикла был разработан оптимизированный публично доступный код для расчета четырехпетлевых вакуумных диаграмм [8]. Он позволил в дальнейшем осуществить нетривиальное вычисление контрчленов для всех пятипетлевых диаграмм, необходимых для вывода РГ функций скалярных моделей в шестимерии [9], открыв тем самым новые возможности для РГ анализа в пространстве высших размерностей.
Отметим также, что особенностью представленного цикла работ является востребованность результатов в разных областях современной физики. Нам удалось выйти за пределы стандартных подходов и разработать необходимый набор инструментов, позволяющий неспециалистам в многопетлевых вычислениях использовать ренормгрупповой метод для получения важных физических результатов.
Лаборатория теоретической физики им. Н.Н. Боголюбова имеет давнюю и богатую историю подобного рода вычислений. Начиная с основополагающих работ Н.Н. Боголюбова и Д.В. Ширкова, РГ метод и связанные с ним расчеты многопетлевых диаграмм Фейнмана на протяжении многих лет использовались в ОИЯИ для получения результатов мирового уровня. Среди них можно отметить широко известные работы, посвященные вычислениям в скалярной φ4 и квантовой хромодинамике (КХД). Что касается Стандартной модели (СМ), то большой резонанс в литературе вызвали недавние расчеты трехпетлевых РГ функций. После измерения массы бозона Хиггса в 2012 г. они позволили провести наиболее полный и самосогласованный анализ проблемы стабильности вакуума, повлекший за собой бурные дискуссии о возможной нестабильности СМ и необходимости введения Новой физики.
Литература:
[1] Alexander Bednyakov и Andrey Pikelner. Four-Loop Gauge and Three- Loop Yukawa Beta Functions in a General Renormalizable Theory . в: Phys. Rev. Lett. 127.4 (2021), с. 041801. doi: 10 . 1103 / PhysRevLett . 127.041801. arXiv: 2105.09918 [hep-ph].
[2] A. Bednyakov и A. Pikelner. Six-loop beta functions in general scalar theory . в: JHEP 04 (2021), с. 233. doi: 10 . 1007 / JHEP04(2021 ) 233. arXiv: 2102.12832 [hep-ph].
[3] A. V. Bednyakov и A. F. Pikelner. Four-loop strong coupling beta-function in the Standard Model. в: Phys. Lett. B 762 (2016), с. 151 156. doi: 10.1016/j.physletb.2016.09.007. arXiv: 1508.02680 [hep-ph].
[4] A. V. Bednyakov. On three-loop RGE for the Higgs sector of 2HDM . в: JHEP 11 (2018), с. 154. doi: 10.1007/JHEP11(2018)154. arXiv: 1809. 04527 [hep-ph].
[5] A. Bednyakov и A Pikelner. Four-loop QCD MOM beta functions from the three-loop vertices at the symmetric point . в: Phys. Rev. D 101.7 (2020), с. 071502. doi: 10 . 1103 / PhysRevD. 101 . 071502. arXiv: 2002 . 02875 [hep-ph].
[6] Alexander Bednyakov и Andrey Pikelner. Quark masses: N3LO bridge from RI/SMOM to MS scheme . в: Phys. Rev. D 101.9 (2020), с. 091501. doi: 10.1103/PhysRevD.101.091501. arXiv: 2002.12758 [hep-ph].
[7] Andrey Pikelner. Three-loop vertex integrals at symmetric point . в: JHEP 06 (2021), с. 083. doi: 10. 1007/ JHEP06(2021) 083. arXiv: 2104. 06958 [hep-ph].
[8] Andrey Pikelner. FMFT: Fully Massive Four-loop Tadpoles . в: Comput. Phys. Commun. 224
(2018), с. 282 287. doi: 10.1016/j.cpc.2017.11. 017. arXiv: 1707.01710 [hep-ph].
[9] Mikhail Kompaniets и Andrey Pikelner. Critical exponents from ve-loop scalar theory renormalization near six-dimensions . в: Phys. Lett. B 817 (2021), с. 136331. doi: 10.1016/j.physletb.2021.136331. arXiv: 2101. 10018 [hep-th].
Информация и фото предоставлены пресс-службой Объединенного института ядерных исследований