Самарские физики занимаются исследованием немарковской динамики и предлагают альтернативный вариант, применяя численное решение нелинейного стохастического уравнения Шрёдингера. Это важно для понимания свойств твердотельного квантового компьютера.
Математическую основу для поиска и изучения источников квантовой коммуникации и квантового компьютинга составляет теория открытых квантовых систем. Она позволяет получить аналитические модели, пригодные для квантовых вычислений.
Одним из возможных подходов для описания динамики открытых классических систем является использование учеными стохастического уравнения Шрёдингера. Применив его, можно вывести так называемое, марковское или немарковское приближение, следовательно, изучить эффекты памяти, связанные с динамикой окружения. В то время как большинство специалистов ищет общую форму немарковского кинетического уравнения, все преимущества стохастического уравнения Шрёдингера остаются малоизученными.
Кроме того, важно исследовать и описать поведение квантовой системы и ее взаимодействие с внешней средой. К такого рода системе причисляют микромеханические резонаторы, квантовые точки, сверхпроводящие кубиты, источники одиночных фотонов, необходимые для квантовой коммуникации. Проблема в том, что не все квантовые системы могут быть описаны посредством традиционных методов. Специалисты предлагают свои варианты решения задач, лежащих в области квантовой информатики.
На фото – Семин Виталий Владимирович – кандидат физико-математических наук, доцент кафедры наноинженерии факультета электроники и приборостроения Самарского национального исследовательского университета имени академика С.П. Королёва
Самарские ученые в рамках двухлетнего проекта (с 2018 по 2020 гг.) по гранту РФФИ «Исследование влияния эффектов немарковости на динамику открытых квантовых систем» математически вывели уравнения динамики немарковских открытых квантовых систем.
Так, российские физики-теоретики путем моделирования и численных расчетов выбрали модели и предложили для каждой свое решение, учитывая разные факторы воздействия. Изучив эффекты немарковского случая, они проанализировали динамику возбуждения различных квантовых состояний системы. Специалисты рассмотрели модель кубита в лазерном поле в немарковском окружении и влияние его параметров на динамику модели.
Виталий Владимирович Семин – руководитель проекта, кандидат физико-математических наук, доцент кафедры наноинженерии факультета электроники и приборостроения Самарского национального исследовательского университета имени академика С.П. Королёва – сообщил об основных положениях проводимого исследования.
«Сначала стоит пояснить, что мы понимаем под марковостью и немарковостью. Данные понятия всегда относятся к динамике систем, другими словами, системы должны изменяться со временем. Если данные изменения в настоящий момент времени не зависят от прошлых состояний системы, то говорят, что система марковская или без памяти, иначе - немарковская или с памятью.
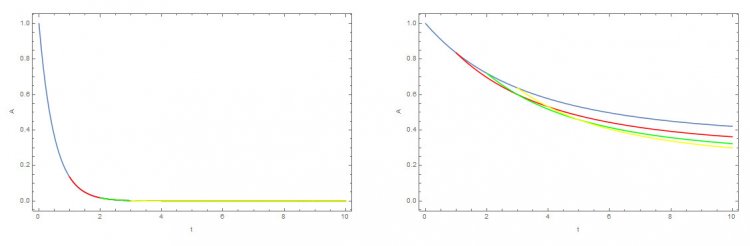
На Рис. 1 (слева) изображена некая характеристика марковского процесса: хорошо видно, что начиная с разных начальных условий, характеристика развивается по одному и тому же закону (отмечено разными цветами). Для немарковского процесса (справа) новое начальное условие приводит к полному изменению динамики развития характеристики.
Виталий Семин раскрыл суть обозначенных понятий и пояснил, какое значение имеет изучение немарковских состояний для применения в квантовых системах связи:
Рисунок 1. Марковский и немарковский процесс
Ясно, что марковские системы являются некой идеализацией и в природе в чистом виде не встречаются. Особенно существенно проявление памяти на коротких масштабах времени, скажем, порядка наносекунд, для таких масштабов марковское приближение неприменимо в принципе. Поскольку квантовые преобразователи или вентили действуют на сверхкоротких временах, то учет немарковости важен для более полного понимания их работы и более точного предсказания конечных состояний квантовых регистров после их действия. Для квантовых систем связи немаловажным является среда, через которую передается сигнал, и здесь снова действие среды на наш сигнал может быть немарковским и наличие теории для описания распространения сигнала в среде с памятью является важным».
В ходе данного проекта самарские специалисты исследовали четыре модели. В 2018 г.: 1) модель двухуровневого атома в немарковском окружении, которое описывается стохастическим процессом Орнштейна-Уленбека, взаимодействующего с лазерным полем, при конечной температуре; 2) модель двух взаимодействующих двухуровневых атомов в немарковском окружении при конечной температуре. В 2019 г.: 1) модель трехуровневого атома в немарковском окружении, взаимодействующего с двумя лазерными полями; при этом лазерные поля будут содержать случайный шум; 2) модель двух взаимодействующих двухуровневых атомов в немарковском окружении в "шумящем" лазерном поле.
Вывести немарковские стохастические уравнения для этих моделей и их прямое компьютерное моделирование – были основными задачами физиков.
«В каком-то смысле это продолжение работ, начатых за несколько лет до этого, связанных с изучением немарковских систем. Несколько лет назад я обнаружил подход к таким системам, основанный на стохастических уравнениях. Данный проект является естественным развитием идей описания квантовых систем с помощью таких уравнений», - отметил Виталий Семин.
Поэтому приоритетным, по словам самарского ученого, стало исследование немарковской динамики низкоразмерных квантовых систем, таких как отдельные двух- и трехуровневые атомы и группы из их небольшого числа, во внешних термических и лазерных полях с помощью стохастического уравнения Шрёдингера.
Под руководством Виталия Семина в проекте принимали участие обучающиеся в Самарском национальном исследовательском университете имени академика С.П. Королева аспирант Андрей Павельев и магистрант Даниил Васильев, которые проводили численный эксперимент.
Так, самарские специалисты провели анализ динамики возбуждения различных квантовых состояний системы и предложили свое описание немарковского случая, опираясь на нелинейное стохастическое уравнение Шрёдингера (ИССЛЕДОВАНИЕ НЕМАРКОВСКОЙ ДИНАМИКИ ДВУХ ВЗАИМОДЕЙСТВУЮЩИХ КУБИТОВ НА ОСНОВЕ ЧИСЛЕННОГО РЕШЕНИЯ НЕЛИНЕЙНОГО СТОХАСТИЧЕСКОГО УРАВНЕНИЯ ШРЁДИНГЕРА. //КОМПЬЮТЕРНАЯ ОПТИКА, 2019, ТОМ 43, ВЫПУСК 2, 168–173). Физики пришли к выводу, что немарковость оказывает существенное влияние на динамику системы, в частности, на вероятность возбуждения перепутанных состояний.
В чем состоит разница в марковском и в немарковском случаях?
«Если просто, то в данном случае марковская и немарковская динамика означает, что система кубитов помещена в некую среду, которая влияет на процессы, происходящие с кубитами. Если отклик среды на изменение состояния кубитов мгновенен, то система марковская, если среда реагирует в течение конечного времени – то система немарковская. То есть марковские системы в чистом виде в природе не встречаются, среда всегда реагирует на изменения в системе не мгновенно, а в течение некоторого времени, –
отвечает Виталий Семин и объясняет, в чем проявляется немарковская динамика системы, –
В данной работе немарковость существенно меняет характер динамики процесса релаксации системы. В частности, можно указать следующие заметные эффекты в немарковском случае: изменяются равновесные состояния системы кубитов, замедляется скорость перехода к равновесию, наблюдается конечная вероятность возбуждения так называемых перепутанных состояний».
В чем преимущество вашего метода моделирования динамики немарковской системы кубитов?
По мнению Виталия Семина, «это технический вопрос, который требует пояснения множества деталей. Если кратко, то замечу, что существует множество подходов к описанию динамики в немарковских квантовых системах. Многие подходы, кроме чрезвычайной сложности, могут приводить к нефизическим уравнениям, которые предсказывают, например, отрицательную вероятность какого-то события. Таким вероятностям крайне трудно придать хоть какой-то физический смысл. Возможны и такие ситуации, когда подход работает для одного набора параметров и полностью «ломается» для другого, что также может свидетельствовать о недостатке конкретного метода. В нашем подходе такие ситуации исключены полностью, что и отличает его от многих других. Другое преимущество нашего метода – это размерность уравнения, которая оказывается существенно меньше, чем в других подходах. Таким образом, в принципе, наш метод позволяет описывать системы, состоящие из достаточно большого числа частиц».
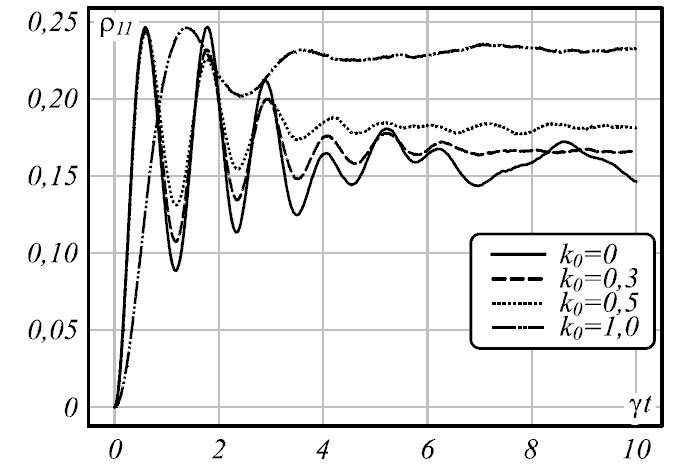
Далее специалисты рассмотрели модель кубита в лазерном поле и изучили влияние на нее немарковости окружения (ИССЛЕДОВАНИЕ ДИНАМИКИ КУБИТА ВО ВНЕШНЕМ ПОЛЕ ЛАЗЕРА// КОМПЬЮТЕРНАЯ ОПТИКА, 2019, ТОМ 43, ВЫПУСК 4, 562–566). Полученное уравнение позволяет учитывать изучение влияния собственного шума лазера на динамику системы также в её немарковском окружении, что подтвердили результаты численного моделирования.
«Шум в нашем исследовании вводился в частоту излучения лазера, параметр k указывает на интенсивность шума. Не углубляясь в технические детали, скажем, что увеличение интенсивности такого шума в лазере приводит к ослаблению его влияния на квантовый объект, что в свою очередь является негативным эффектом, с которым нужно бороться», – подчеркнул Виталий Семин.
Рисунок 2. Представлено влияние собственного шума лазера и изображена вероятность обнаружить кубит в невозбужденном состоянии с течением времени
Как немарковость влияет на динамику кубита?
«Этого никто не знает. Как я уже говорил, существует множество подходов к описанию немарковской динамики и все они что-то предсказывают. Согласно нашим результатам, самый заметный эффект присутствия памяти в динамике кубита – это изменение равновесного состояния. Другими словами, через определенный промежуток времени система приходит к равновесному состоянию, которое в марковском и немарковском случае имеет различные значения. Кроме того, скорость такого перехода к равновесию в немарковском случае медленнее, что в итоге должно приводить к сужению спектральных линий излучения такого кубита», – считает Виталий Семин.
Основной упор ученые сделали на размерность уравнения, что работает для разных квантовых систем и позволяет строить модели с разными параметрами, наблюдая их влияние на динамику этих систем.
Таким образом, проект, посвящённый изучению такого вопроса математической физики, как анализ квантового кинетического уравнения, так называемых эффектов памяти (или немарковость), станет новой ступенью в развитии теоретических основ квантовых компьютеров.