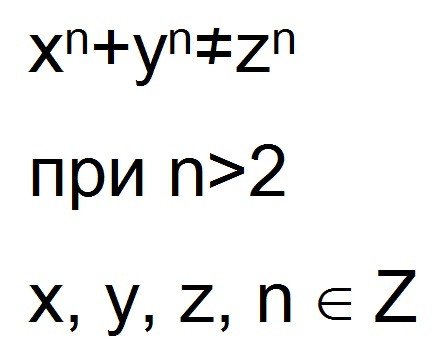Как человек, который постоянно отслеживает новости науки, могу уверенно сказать — новости об открытиях и исследованиях в математике приходят редко. Возникает ощущение, что в физике или биологии что ни день, то открытие, а математика — это Перельманы раз в десятилетие. Чем занимаются современные математики, что важного происходит в этой науке и почему мы так мало о ней знаем — обо всем этом мы спросили математиков и популяризаторов этой науки.
На вопросы Научной России отвечали:
— заведующий лабораторией популяризации и пропаганды математики Математического института им. В. А. Стеклова, кандидат физико-математических наук, лауреат премии «Просветитель» 2015 года Николай Андреев.
— доктор физико-математических наук, сотрудник МФТИ, РЭШ, ЦЭМИ РАН, автор более ста научно-популярных курсов по математике Алексей Савватеев.
Сложности популяризации математики
«Сегодняшние открытия часто делаются на тех ступенях, которые нельзя объяснить простым людям. А вот то, что происходит на уровне простого языка, то и попадает в новости. Обычно это великие открытия. Если открытие сделано в задаче, которую можно сформулировать простым языком, это великое открытие», — говорит Алексей Савватеев.
Несмотря на то, что все мы в школе, хотели мы того или нет, занимались математикой очень много, мы не изучили и сотой доли всех тех понятий и даже общих закономерностей, что существует в этой науке. А значит, уже начав разбираться с каким-то исследованием, мы натолкнемся на то, что не понимаем даже слов, что употребляет ученый.
«Для объяснения любого открытия придется ввести очень много контекста, а в некоторых областях много определений уже на начальном этапе, чтобы в итоге дойти до сути. В общем, входной билет очень дорогой», — говорит Николай Андреев.
Сложно, но не невозможно. Пример тому — и блестящие книги по математике для широкого круга читателей, одну из которых — «Математическая составляющая» — жюри «Просветителя» признало лучшей в 2015 году. В книге, над которой работал большой авторский коллектив, действительно, достаточно понятным языком рассказывается о работе математиков. Появляются и курсы по математике для всех желающих, где основы этой науки лекторы стараются донести даже до самых ярко выраженных гуманитариев, причем они оказываются неожиданно популярны — так, на онлайн-курс Алексея Савватеева к его собственному удивлению записалось несколько тысяч человек.
Одна из главных сложностей с популяризацией математики связана с тем, что исследования в этой науке очень редко удается ярко визуализировать. «Если вы придете в любой музей науки, вы увидите, что там физических, химических, биологических экспонатов много, а математических — почти нет», — говорит Николай Андреев. Тем не менее, эту задачу уже давно и вполне успешно решает проект Андреева «Математические этюды».
Еще одна сложность, о которой говорят многие математики, занимающиеся популяризацией — страх перед этой наукой, укоренившийся у многих еще со школы. Отчасти он связан с проблемами преподавания математики в школе, а отчасти со вполне объективной сложностью этой науки.
«Математика постоянно на всех уровнях требует очень высокого понимания. Если ты не понял, как дроби складывать, то и дальше сложно будет», — говорит Николай Андреев.
«Это ступень за ступенью постижение. И каждая ступень — это огромные усилия над собой, каждый отпадает на своей ступени. Это, действительно, вызов для интеллекта, ведь математика — это, можно сказать, концентрированная сложность мира. А мир — он так устроен, он сложный, потому и математика сложная», — добавляет Алексей Савватеев.
Революция, которую никто не замечает
«За последние несколько десятилетий математиками доказано, как минимум, три величайшие гипотезы, сняты проблемы, стоявшие столетиями. Я считаю, что в математике происходит самая настоящая революция, только ее никто не замечает», — говорит Алексей Савватеев.
Итак, великие открытия, которые мы не заметили — это Проблема четырех красок, Великая теорема Ферма, Гипотеза Пуанкаре и проблема узлов. Памятуя о сложностях перевода с математического языка на русский обывательский, попробуем хотя бы кратко рассказать о том, что это за открытия.
Теорема о четырех красках была сформулирована в 1852 году и доказана только в 1976 году, став, кстати, первой значимой теоремой, доказанной при помощи компьютера. Согласно этой теореме, всякую расположенную на сфере карту можно раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета.
Гораздо дольше своего доказательства ждала Великая теорема Ферма, о которой многие слышали из школьного курса математики. Знаменитый математик сформулировал ее в 1637 году буквально на полях книги — «Арифметики» авторства Диофанта, древнегреческого математика III века до н.э. Он даже сумел невольно подразнить своих поздних коллег, написав, что придумал весьма остроумное доказательство теоремы, но не помещает его сразу, ибо оно слишком длинно, чтобы поместиться на полях книги. Впрочем, скорее всего, в его доказательстве была ошибка, потому что математический аппарат, позволивший в конце концов эту теорему все-таки доказать, — в 1994 году, — появился в основном только в XX веке.
Формулировка этой теоремы такова: для любого натурального числа n со значением больше 2, уравнение an+bn=cn не имеет решений в целых ненулевых числах a, b, c. Увы, 130-страничное доказательство теоремы мы здесь привести не можем.
Про гипотезу Пуанкаре многие впервые услышали в 2006 году, когда все СМИ мира написали про российского математика Григория Перельмана. Он сделал открытие, названное журналом Science «прорывом года» (впервые для математики), стал Филдсовским лауреатом, но отказался от этой и других премий, а также любой публичности. Собственно, это все, что мы знаем о гипотезу Пуанкаре, поскольку сама она для понимания действительно очень сложна. Гипотеза, сформулированная в 1904 году, гласит, что «всякое односвязное компактное трехмерное многообразие без края гомеоморфно трехмерной сфере».
Математика и жизнь
Это, безусловно, еще одно отличие математики от большинства наук. Рассказывая об открытии в биологии, ученый почти всегда может сказать, где оно может пригодиться в ближайшем будущем — изобретем новое лекарство, узнаем секрет долголетия. Физик расскажет о том, что его работа приведет к созданию новых батарей, химик пообещает новые эффективные материалы и так далее. Математик на такой вопрос, чаще всего, ответить не сможет, да и не захочет отвечать.
«Если человек задает себе вопрос, зачем это нужно, значит, он уже не математик. Я никогда не отвечаю студентам на этот вопрос, — говорит Алексей Саватеев. — Ты никогда в жизни не узнаешь, что нужно, а что не нужно. Когда Минковский разрабатывал правила действия, он и в мыслях не имел, что это теория относительности. 30 лет прошло, и оказалось, что это вовсе не работа в стол».
Можно сказать, что именно благодаря таким историям, математики и завоевали себе мощный кредит доверия, чтобы не приходилось бесконечно отвечать на вопросы о «прикладном значении» их работы. Оно всегда очевидно по факту, за множеством потрясающих примеров можно обратиться ко все той же книге «Математическая составляющая».
«У нас в книжке есть примеры, когда какие-то вещи, которыми занимались математики, входили в практику через столетие — например, геометрия Лобачевского. И есть примеры, когда практически сразу, так, например, происходит с криптографией», — рассказывает Николай Андреев.
Кроме того, в ходе доказательства любой большой теоремы попутно всегда разрабатывается инструментарий, который потом применяется и в других сферах. «Так было, например, с теоремой Ферма, сейчас активно применяются методы, разработанные для ее доказательства, математика уже иначе развивается», — поясняет Андреев.
«Задачи Пола Эрдеша [о решении одной из них недавно писал наш портал] до сих пор решают просто потому, что они красивые! Но в то же время если ты задачи Эрдеша решаешь, то ты и алгоритмы хорошо напишешь — а это антиспам, например, и многое другое», — говорит Алексей Савватеев.
Если хорошенько порасспрашивать математиков, то о разных прикладных задачах, где полезна их наука, можно узнать очень много — от оптимального укладывания вещей в рюкзаке и победы в «Бегущем городе» за счет математически выверенного маршрута до грамотной организации аукционов и игры на бирже. Но, похоже, что для самих математиков все это, на самом деле, побочный эффект, а самое главный двигатель великих открытий — это научный азарт в его самом лучшем виде.