Все, везде и сразу. Квантовые объекты и движение по всем траекториям

У любого объекта в одинаковых условиях может быть только одна траектория. Это просто как дважды два. Брошенный камень полетит по предсказуемой параболе; лазерный луч, направленный в воду, будет преломляться предсказуемым образом. Однако этот закон не распространяется на квантовые объекты — мельчайшие «кирпичики» нашего мира. Но что тогда происходит там, на квантовом уровне? Значит ли это, что мир живет сразу по двум наборам правил, в зависимости от размера? В этом корреспондент «Научной России» постарался разобраться при поддержке ученого — доктора физико-математических наук Алексея Семихатова.

«В классической механике — той, к которой мы привыкли (механике летящего камня, движущейся планеты и других макрообъектов), — движение тел описывается дифференциальными уравнениями. Эти уравнения, известные как законы Ньютона, определяют, как каждое тело в каждый момент времени реагирует на то, как его толкают: это позволяет вычислить ускорение, а затем и траекторию движения», — приступил к объяснению ученый.

Я включаю лазер и направляю его в воду. Луч движется по прямой, пока не встречает новую среду, затем преломляется и добирается до дна аквариума. Если измерить время, затраченное светом на преодоление этого пути, окажется, что такой путь — оптимальный, самый быстрый. Ну и что, спрошу я. Разве это не естественно?

«Да, законы Ньютона математически выражают, как причины (воздействия) вызывают движение. Но те же самые уравнения можно сформулировать альтернативным способом — через принцип наименьшего действия. Представьте: тело движется из точки А в момент времени t₁​ в точку Б в момент t₂​. Между этими событиями существует бесконечное множество возможных траекторий. Однако в реальности тело выбирает лишь одну (например, снаряд, выпущенный под углом к горизонту, летит по параболе, а не по произвольной кривой). Эта траектория соответствует минимуму действия — физической величины, вычисляемой для каждого пути. Оба подхода — через уравнения Ньютона и через действие — математически эквивалентны, но второй открывает путь к обобщениям в квантовой теории и теории поля», — продолжил А.М. Семихатов.

Действие в физике — это своеобразная «всемирная лень». Оно определяется как разность между кинетической и потенциальной энергией системы. Эти два вида энергии лежат в основе механики.

1. Кинетическая энергия — энергия движения. Чтобы разогнать объект (например, бросить камень), необходимо приложить силу.
2. Потенциальная энергия — энергия взаимодействия (например, гравитационного или электромагнитного).

Концепция минимального действия оказалась универсальной. Даже для сложных систем, таких как электромагнитное поле (развитие которого во времени описывается намного более сложно, чем полет камня), удается записать действие. Его минимизация приводит к уравнениям Максвелла, описывающим электродинамику. Аналогично выводятся уравнения Эйнштейна для гравитационного поля, хотя здесь связь с кинетической и потенциальной энергией несколько замаскирована.

«Теперь обратимся к квантовой механике. Это непредставимый мир, где объекты не движутся по определенным траекториям. Именно поэтому, кстати, я воюю с эмблемой Международного агентства по атомной энергии (МАГАТЭ), на которой изображены электроны, летящие по орбитам вокруг ядра. В действительности же электроны не летают по орбитам. Для квантовых объектов принципиально невозможно одновременно иметь точное положение в пространстве и точную скорость. Это отражено в принципе неопределенности Гейзенберга. Поэтому сама концепция траектории в квантовой механике теряет смысл. Здесь хочется задать вопрос: “Но если электроны не летают по траекториям, то что же они делают?” Квантовая механика, однако, обходится без прямого ответа. Различные интерпретации пытаются нечто по этому поводу высказать, но стандартная квантовая механика фокусируется не на описании “реальности”, а на предсказании результатов экспериментов», — заострил внимание ученый.

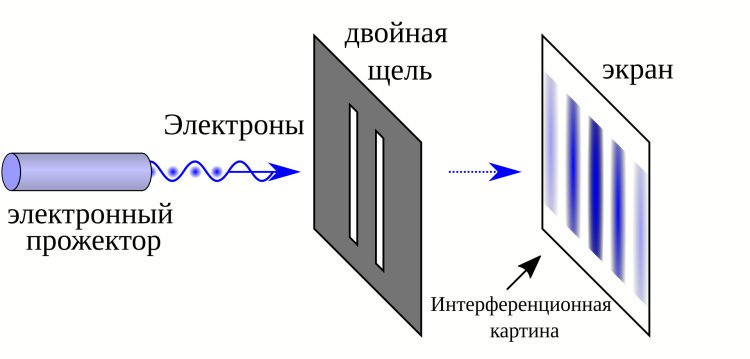
В 1801 г. английским физиком Томасом Юнгом был проведен знаменитый «двухщелевой эксперимент». Суть его проста: есть установка, которая «выстреливает» электроном в считывающий экран. А между установкой и экраном ставят барьер, в котором проделаны две щели. По результатам многократного повторения опыта с выстреливанием электронов поодиночке картина их попадания в экран такова, как будто каждый электрон проходил через обе щели одновременно. При этом мы знаем, что электрон — точечный и неделимый объект. И место на экране, куда попадет каждый отдельный электрон, предсказать нельзя. Максимум, что позволяет нам природа — найти вероятность попадания в тот или иной «пиксель».

«В строго одинаковых условиях одно и то же измерение может давать различные результаты. Квантовая механика определяет лишь вероятности, а предсказать конкретный исход отдельного эксперимента невозможно. Последовательность результатов может выглядеть так: первый, первый, второй, второй, второй, первый, третий и т.д. Однако при проведении тысячи измерений становятся видны закономерности: одни результаты возникают чаще других. Эти эмпирические частоты соответствуют вероятностям, которые извлекаются из формализма квантовой механики. Вся ее математическая структура направлена на расчет именно таких вероятностей. Механизм тут довольно хитрый. Сначала, используя уравнение Шредингера, определяют так называемые амплитуды вероятности — комплексные числа, которые сами по себе не представляют вероятностей (ведь вероятность должна быть положительной величиной в диапазоне от 0 до 1). А чтобы получить вероятность из амплитуды, надо возвести ее модуль в квадрат», — объяснил А.М. Семихатов.

Представим себе «шарик» электрона, который вылетает из установки и добирается до барьера с двумя щелями. Разум человека, привыкший к объектам вроде камня или мяча, которые движутся только по одной траектории, предполагает, что электрон, оказавшись перед барьером, в большинстве случаев будет «выбирать» щель, которая потребует меньше затрат энергии. Почему же иногда электрон будет проходить через другую щель? Предположим, что электрон «проверяет» и этот второй путь и каким-то образом делает это одновременно с тем, как «проверяет» первый путь.

«Основная задача уравнения Шредингера — вычисление амплитуд вероятностей. Однако существует альтернативный подход, исторически восходящий к Полю Дираку и значительно развитый Ричардом Фейнманом. Последний неоднократно подчеркивал, что его метод интегрирования по траекториям основывался на ранних идеях Поля Дирака. Амплитуды вероятности можно получить принципиально иным способом — через учет всех возможных путей системы между состояниями, что стало краеугольным камнем современной квантовой теории. Для этого необходимо рассмотреть все возможные пути, ведущие из начального события к конечному, в более сложных случаях — от начальной конфигурации к конечной. Для каждой мыслимой траектории, которая теоретически может их соединять, требуется рассчитать соответствующее действие. Затем следует взять специальную функцию от этого действия (умножить на мнимую единицу, поделить на постоянную Планка и взять экспоненту) и просуммировать такие вклады от всех траекторий. По математическим причинам такой подход оказывается эквивалентным решению уравнения Шредингера. Полученная сумма дает искомую амплитуду вероятности — скажем, обнаружения электрона в заданной точке», — продолжил объяснение ученый.

Теперь представим себе электрон, рисующий в воздухе множество траекторий, по которым мог бы полететь. Часть проходит через первую щель, а другая часть — через вторую. «Шарик» электрона уже перестает быть похожим на «шарик». Скорее можно представить себе гонку множества «шариков», которые проверяют каждый возможный путь одновременно, и в конце концов кто-то приходит к финишу первый. Этого «победителя» и фиксирует экран. Но… почему победитель не всегда один и тот же? Точнее, почему именно на квантовом уровне победители разные, а на нашем привычном мяч или камень так себя не ведут?

«Этот метод называется интегралом по траекториям, или фейнмановским интегралом — как вам удобнее. Это прекрасный способ вычисления. Рассуждения о том, что при этом “происходит”, — это уже интерпретации», — подводит итог А.М. Семихатов.

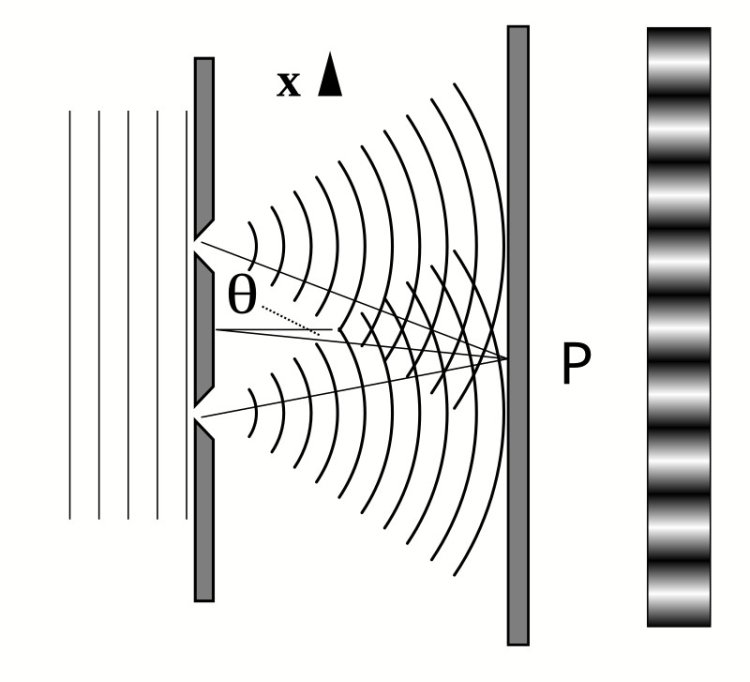
Получается, что на первый вопрос «почему так происходит, что электрон не всегда следует по одной и той же траектории и не всегда оказывается в одном и том же месте» дать ответ мы пока не можем. Одна из интерпретаций такова, что электрон и не выбирает вовсе никакой путь, а просто летит сразу по всем возможным и с какой-то вероятностью оказывается в том или ином месте. Представим снова двухщелевой эксперимент. Из точки, где вылетел электрон, в точку его соударения с экраном проходят множество траекторий: какие-то — через первую щель, какие-то — через вторую. Теперь представлю, что щелей не две, а три. Траекторий прибавилось, и электрон может проследовать по любой из них с какой-то вероятностью. Потом представим, что щелей не три, а пять, десять, сто, тысяча…, пока, наконец, их не станет бесконечно много. И барьеров между установкой и экраном представим не один, а два, три, сто, миллион, бесконечно много. По этой логике электрон должен будет следовать по всей бесконечности возможных траекторий — где-то с большей, а где-то с меньшей вероятностью. То есть дело вовсе не в барьере. Барьер лишь изменял вероятности некоторых исходов.

Однако все еще можно попытаться объяснить, из-за чего макрообъекты не ведут себя так же. Ответ кроется в постоянной Планка, уже упоминавшейся выше. Вклады многих траекторий оказываются существенными, только когда действие, вычисленное для каждой траектории, не слишком велико по сравнению с постоянной Планка. А для волейбольного мяча, в отличие от электрона, это действие огромно, и вклад по существу дает только одна траектория — та, на которой действие минимально. Таким образом и получается привычное нам движение по вполне определенной траектории (вклады всех остальных гасят друг друга).

Несмотря на всю кажущуюся фантасмагоричность квантовой механики, способность ученых описывать поведение этих странных объектов приносит весьма конкретные практические плоды. Прогресс в разработке квантовых компьютеров показал, что они способны проводить вычисления, которые недоступны самым мощным классическим суперкомпьютерам. Так, исследователи из Физического института им. П.Н. Лебедева РАН (ФИАН) и Российского квантового центра (РКЦ) одни из первых в мире продемонстрировали решение прикладных задач на квантовом компьютере. В ходе эксперимента они использовали процессор на основе ионов иттербия (Yb+) и разделили с его помощью написанные от руки изображения нуля и единицы, а также математических объектов — графов. Было показано, что даже небольшие квантовые процессоры уже могут решать простые, но практически значимые задачи, такие как классификация изображений. Это большой шаг к будущему, где квантовые процессоры будут выполнять более сложные вычисления.

Для достижения цели были задействованы алгоритмы машинного обучения, реализованные на квантовом процессоре. Как объяснили исследователи, в работе был применен метод SVM (support vector machine) — это популярный для задач классификации метод машинного обучения. Он помогает разделять данные на классы посредством проведенной между ними оптимальным образом нелинейной границы. «Ядерную часть» алгоритма (сравнение данных) выполняли на квантовом процессоре. Это позволило эффективно обрабатывать даже сложные изображения.

По словам директора ФИАН академика Николая Николаевича Колачевского, в дальнейшем, по мере развития, подобная технология квантовой классификации сможет применяться для множества практических задач. Например, в медицине ее можно использовать для автоматического анализа рентгеновских снимков и данных МРТ и КТ, что поможет оперативно диагностировать заболевания. «В области генетики и биоинформатики квантовые алгоритмы смогут проверять последовательности ДНК, выявляя мутации и предсказывая их влияние на организм. Вместе с тем химия получит инструмент для поиска новых молекулярных структур и моделирования каталитических процессов. В то же время в финансовой сфере квантовые алгоритмы смогут находить сложные закономерности в рыночных данных, улучшая прогнозирование и снижая риски», — пояснил ученый.

Источник изображения на главной и на странице: Freepik

Материал подготовлен при поддержке Министерства науки и высшего образования РФ