Уральские физики-теоретики Института физики металлов (ИФМ) УрО РАН (г. Екатеринбург) занимаются исследованием сингулярностей ван Хова в электронном спектре кристаллических решеток. Это позволит выяснить причину сильных аномалий термодинамических свойств, которые важно учитывать в различных прикладных направлениях физики твердого тела
Для исследований магнитных и электронных свойств в разных микроскопических моделях в расчет берутся свойства материалов с конкретной плотностью состояний, в которой часто возникают особенности или сингулярности ван Хова.
Сингулярности ван Хова могут приводить к сильным аномалиям температурных зависимостей термодинамических свойств. Важно изучить их природу, так как она влияет на электронное и магнитное взаимодействие в веществах. Например, для трехмерных (кубических) и низкоразмерных решеток формируются разные сингулярности ван Хова.
Специалисты предлагают свои варианты математических решений, чтобы дать описание особенностей ван Хова, существенных для магнитной и сверхпроводящей нестабильностей. Российские физики-теоретики путем компьютерных и аналитических расчетов предложили свой вариант исследования, рассмотрев сингулярности плотности состояний для разных решеток (квадратной и кубических), и выполнили детальный топологический анализ линий и поверхностей ван Хова.
На фото – Ирхин Валентин Юрьевич – доктор физико-математических наук, заведующий лабораторией квантовой теории конденсированного состояния Института физики металлов имени М.Н. Михеева Уральского отделения РАН (ИФМ УрО РАН) (г. Екатеринбург)
Сотрудники Института физики металлов имени М.Н. Михеева Уральского отделения РАН (ИФМ УрО РАН) (г. Екатеринбург) – Валентин Юрьевич Ирхин – доктор физико-математических наук, заведующий лабораторией квантовой теории конденсированного состояния и Петр Алексеевич Игошев – кандидат физико-математических наук, старший научный сотрудник лаборатории квантовой теории конденсированного состояния – рассказали, что представляют собой сингулярности ван Хова, каково их значение для объяснения сильного магнетизма переходных металлов, а также как теоретические расчеты и формулы могут точно определить особенности и аномалии электронных и магнитных свойств в различных кристаллических решетках.
Что такое сингулярности ван Хова в электронном спектре и как они формируются?
После обсуждения между собой ученые ответили: «Из школьного курса физики известно, что инерционные свойства тела (“материальной точки”) зависят только от его массы. Для электрона в твердом теле ситуация существенно усложняется: инерция будет зависеть и от направления ускорения, и от значения импульса. Причиной усложнения является влияние кристаллической решетки, которая драматически изменяет электронный спектр (энергию) электрона. И если для свободного электрона импульсы, соответствующие данной энергии, т.е. лежащие на изоэнергетической поверхности, всегда образуют сферу в пространстве импульсов, то в твердом теле это могут быть достаточно причудливые образования, форма которых существенно варьируется с изменением энергии.
Сингулярность ван Хова в твердом теле возникает, когда энергия электрона в данной области импульсного (обратного) пространства слабо зависит от его импульса (точнее, квазиимпульса, периодически определенного в пространстве так называемой обратной решетки). Леон ван Хов строго доказал еще в 1953 году: каким бы ни был электронный спектр, всегда найдутся значения вектора квазиимпульса (точка), вблизи которых он меняется медленно. Есть три типа таких точек – минимум; максимум; минимум в одних направлениях, а максимум – в других (так называемая седловая точка ван Хова). Изменение связности поверхности с изменением энергии или других параметров (топологический переход) обычно происходит в особом случае, когда эта поверхность содержит в себе линию ван Хова, в окрестности которой спектр особенно слабо зависит от квазиимпульса. Фактически, эта линия получается из-за слияния нескольких точек ван Хова при топологическом переходе. Здесь требуется аккуратный топологический анализ, за которым следует численный расчет.
На фото – Игошев Петр Алексеевич – кандидат физико-математических наук, старший научный сотрудник лаборатории квантовой теории конденсированного состояния Института физики металлов имени М.Н. Михеева Уральского отделения РАН (ИФМ УрО РАН) (г. Екатеринбург)
Несколько точек ван Хова существуют для любого спектра в твердом теле – это следствие теоремы ван Хова – однако в трехмерном случае их самих по себе недостаточно для возникновения аномалий и фазовых переходов. Для этого необходимо или формирование очень «тяжелых» точек ван Хова, в окрестности которых спектр меняется особенно медленно, или слияние нескольких таких точек, что приводит к формированию целой линии ван Хова».
Какое значение имеет изучение аномалий термодинамических свойств в физике твердого тела и какую роль в этом случае играет присутствие сингулярностей ван Хова?
Авторы снова отреагировали вместе: «Аномалии термодинамических свойств твердых тел (высокие значения их важных физических характеристик: теплоемкости, магнитной восприимчивости, упругих свойств, термоЭДС и т. д., а также их сильные температурные зависимости) приводят к ряду наблюдаемых эффектов, в том числе к структурным и магнитным фазовым переходам. Тем самым, они играют огромную роль в практических и технических приложениях физики твердого тела. Очень многие свойства металлов определяются тем, насколько плотно электронные состояния группируются вокруг граничной энергии электронов проводимости (она называется энергией (уровнем) Ферми EF). Обсуждаемые аномалии могут иметь два источника. Во-первых, это корреляционные эффекты – электрон настолько активно участвует во взаимодействии с другими электронами, что это приводит к его утяжелению (вокруг него как бы формируется целое электронное облако) и сильному рассеянию при удалении от уровня Ферми. Кроме того, решетка может так воздействовать на отдельные электроны, что их энергии плотно группируются в узком интервале вокруг EF, а их импульсы – в слое вблизи поверхности Ферми. Поверхность Ферми в твердом теле существует всегда, но сильное накопление электронов вблизи EF – только в присутствии сингулярностей ван Хова. Таким образом, оба обсуждаемых фактора характеризуются количеством электронов, находящихся вблизи поверхности Ферми, – плотностью электронных состояний ρ(ε), где ε – электронная энергия, обычно отсчитываемая от EF. Эта величина и может проявлять сингулярное поведение; в широком смысле под этим понимаются кинки (изломы производной) и корневое поведение, в узком смысле – обращение ρ(ε) в бесконечность,
Сингулярности ван Хова имеют решающее значение для объяснения сильного магнетизма переходных металлов. В частности, в самой распространенной альфа-фазе железа (с объемноцентрированной кристаллической структурой) существенную роль по-видимому играет линия ван Хова, обозначаемая как ГN(D) (для точек обратного пространства твердого тела существует специальная номенклатура обозначений). В никеле ситуация другая – причиной магнетизма является точка ван Хова L. Эта же точка важна для слабого ферромагнетизма соединения ZrZn2. Такие сингулярности важны для многих электронных и решеточных свойств, обеспечивая высокую электронную теплоемкость, определяя упругие модули и задавая структурные и магнитные фазовые переходы».
В основе теоретической базы для исследования эффекта ван Хова уральские ученые Института физики металлов брали аналитические и численные компьютерные расчеты в рамках одноэлектронной зонной картины твердого тела.
Как отмечают авторы исследования, «выполняя аналитические вычисления, мы использовали формализм специальных функций – так называемых эллиптических интегралов. При этом удивительным образом возникают аналогии с кеплеровскими законами движения планет, объясненными Ньютоном на основе закона всемирного тяготения и лежащими в основе астрономии. Правда, в нашем случае орбиты располагаются не в реальном (прямом, координатном), а в квазиимпульсном (то есть обратном) пространстве. Дело в том, что обычный координатный язык неудобен для микроскопического описания практически всех электронных свойств, за исключением электронной плотности. Вместо этого удобно говорить, что электрон «движется» (в квазиклассическом смысле) в пространстве импульсов, находясь на поверхности с фиксированной энергией. Как планета движется по замкнутой орбите, ускоряясь и разгоняясь, так и электрон изменяет свой импульс, находясь на замкнутой стационарной орбите. Средний (по всевозможным орбитам – сечениям поверхности) «период» обращения электрона и равен плотности электронных состояний, соответствующей данной энергии. Как и в задаче Кеплера, при изменении параметров происходит переход от замкнутых к открытым орбитам».
В своей работе, опубликованной в международном журнале PHYSICS OF METALS AND METALLOGRAPHY, 2019, VOL. 120, NO. 13, при рассмотрении точек и линий ван Хова ученые выявляют особенности и аномалии электронных и магнитных свойств в кубических решетках. Что удалось определить физикам?
Валентин Ирхин и Петр Игошев дали следующее пояснение: «Электронный спектр можно описывать на языке интегралов переноса (перескока) электронов между орбиталями на разных атомах (узлах), которые численно характеризуют потенциал в области перекрытия электронных орбиталей рассматриваемой пары узлов. В качестве простой и достаточно информативной модели мы учитывали только два ненулевых интеграла переноса. Таким образом, единственным параметром выступает τ – отношение интеграла переноса между вторыми по близости соседями к интегралу для ближайших соседей.
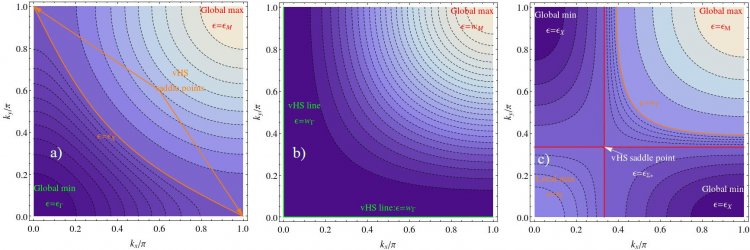
Рисунок 1. Изменение изоэнергетических орбит электрона и седловых точек ван Хова (показаны стрелками; точки минимума и максимума находятся в нижнем левом и верхнем правом углу) с изменением параметра τ для ПК решетки; сечение импульса kz = π/2. Цветом показано значение энергии (спектр). a) τ = 0.3, точки ван Хова - (π,0) и (0,π), орбиты вокруг них открытые. b) τ = 0.5, зеленым цветом показаны линии ван Хова. c) τ = 1.0, орбиты вокруг точек ван Хова (π,0) и (0,π) становятся замкнутыми. Линия ван Хова распалась на точки (0,0), (π,0), (0,π) и точку, выделенную белой стрелкой. С увеличением τ последняя точка движется от точки (0,0) вдоль диагонали
Для трехмерных кубических решеток (всегда существующие) седловые точки ван Хова не могут в одиночку привести к расходимости – обращению ρ(ε) в бесконечность. Однако если такие точки формируют линию, эта расходимость возможна, причем она совпадает с точкой топологического перехода в электронном спектре. Это проявляется и в том, что точка математического фокуса изоэнергетических орбит меняется. Отклонение параметров от этого случая приводит к распаду линии ван Хова на несколько точек ван Хова (две-три), когда ρ(ε) в какой-то мере сохраняет особенности (большая величина и резкая зависимость). На Рис. 1 показан изменение изоэнергетических поверхностей с изменением параметра τ для сечения поверхностей ПК решетки. Видно, что происходит топологический переход при τ = 0.5: формируется линия ван Хова, изменяется тип орбит с открытых на замкнутые.
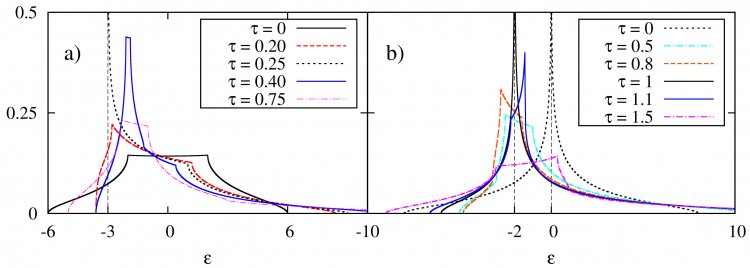
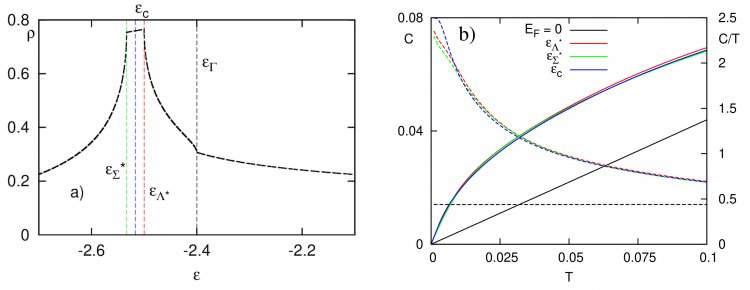
Мы получили точные формулы для ρ(ε) через эллиптические интегралы и построили графики при различных значениях τ для простой кубической (ПК) и объемноцентрированной кубической (ОЦК) решеток (результаты расчета показаны на Рис. 2. Для ПК решетки линия ван Хова возникают при τ = 1/4, что приводит к расходимости типа обратного корня четвертой степени. Если τ > 1/4, эта линия распадается на несколько точек, формирующих симметричное плато (примеры – τ = 0.4 на Рис 2а, τ = 0.3 - на Рис. 3a). Для ОЦК решетки линии ван Хова имеются при τ = 0 (логарифмического типа) и τ = 1 (типа обратного корня четвертой степени). При отклонении τ от этих значений линии ван Хова распадаются на несколько точек, формирующих асимметричное плато (пример – при τ = 1.1) с резким падением ρ(ε). В качестве примера влияния сингулярностей ван Хова на термодинамические свойства на Рис. 3 показан результат расчета электронной теплоемкости для ПК решетки при τ = 0.3 (уровень Ферми расположен на плато). Стандартная теория Зоммерфельда предсказывает линейный рост электронной теплоемкости с ростом температуры в случае, когда уровни сингулярности ван Хова и Ферми не близки. Видно, что наличие сингулярностей ван Хова сильно нарушает результаты теории Зоммерфельда, делая ее по существу неприменимой».
Рисунок 2. График плотности состояний ρ(ε) для различных значений параметра τ. a) ПК решетка, b) ОЦК решетка. Вертикальные пунктиры соответствуют уровням сингулярности ван Хова
В других недавних работах («ПИСЬМА В ЖЭТФ», 2019, «ЖЭТФ», 2019) Ирхин и Игошев изучили переход металл-изолятор для различных решеток (квадратной, ПК и ОЦК):
«Все эти решетки бипартитные, т.е. разбиваются на такие две подрешетки, что ближайшие соседи узлов из одной подрешетки принадлежат другой. В постановке задачи сыграло роль то, что для бипартитных решеток термодинамика системы может быть полностью определена через плотность электронных состояний ρ(ε). Роль сингулярностей ван Хова можно увидеть из сравнения поведения ρ(ε) в окрестности нуля: для ПК решетки при ε = 0, τ = 0 сингулярности нет, а для ОЦК решетки есть (см. рис. 2). При τ = 0 даже самое малое кулоновское взаимодействие приводит к формированию антиферромагнитного состояния, являющегося изоляторным из-за разбиения электронного спектра на две ветви, разделенные энергетической щелью».
Как присутствие сингулярностей ван Хова может решить проблему определения сценария перехода металл–изолятора и почему были выбраны бипартитные решетки?
«Малое изменение электронного спектра при ненулевом τ может привести к фазовому переходу изоляторного состояния как в фазу антиферромагнитного металла (за счет перекрытия ветвей), так и в парамагнитное. Используя асимптотическое разложение ρ(ε) вблизи нулевой энергии, мы можем получить теоретическую зависимость энергии парамагнитной и антиферромагнитной фаз при малых τ на гипотетической границе перехода металл-изолятор. Оказывается, что сингулярность ван Хова приводит к наличию логарифмических вкладов в термодинамические величины. Это может менять род фазового перехода при малом значении параметра τ, что совершенно невозможно для случая несингулярной (гладкой) плотности состояний. Приятной особенностью полученного результата является то, что он практически полностью может быть получен расчетом «на бумаге», без применения вычислительной техники. В дальнейшем мы планируем исследование небипартитных решеток – треугольной и гранецентрированной кубической (ГЦК), в которых важны эффекты фрустраций – конкуренции электронного переноса между разными парами соседей».
Рисунок 3. Влияние плато плотности состояний на температурную зависимость теплоемкости при различных положениях уровня Ферми для ПК решетки при τ = 0.3. a) Плотность электронных состояний, выбор уровня Ферми отмечен цветом. b) Электронная теплоемкость C (сплошные линии) и коэффициент теплоемкости C/T (пунктирные линии). Цветом отмечен различный выбор уровня Ферми соответственно рис. 3а. Для сравнения показан случай, когда уровень Ферми (лежащий в нуле) удален от уровней особенности ван Хова, что приводит к линейной зависимости теплоемкости (теория Зоммерфельда)
Для каких вычислительных методов (квантовых или расчета свойств материалов) может быть полезен проведенный вами анализ особенностей ван Хова?
«Использованный нами метод может применяться в расчетах электронных свойств «из первых принципов» (в частности, в методе функционала плотности, основанном на теореме Хоэнберга-Кона) в тех случаях, когда для исследуемой системы важно наличие сингулярностей ван Хова; такая ситуация как раз обычна для многих переходных металлов и их соединений, в том числе практически важных. Дело в том, что в стандартных первопринципных методах исследования спектра (интегрирование по методу тетраэдров) используется линейное приближение, которое размывает вклад сингулярностей: оно усредняет вклад точки ван Хова, находящейся внутри или в одной вершине тетраэдра с вкладом остальных трех или четырех вершин. Это дает очень грубый, зачастую недостаточный результат для описания фазового перехода. Точный учет формы электронного спектра для случая, когда уровень Ферми находится вблизи сингулярностей ван Хова, позволяет исчерпывающе исследовать критическое поведение и термодинамические свойства в рамках современных подходов теории твердого тела (динамическая теория среднего поля, функциональная ренормгруппа, метод вспомогательных частиц и другие)», – убеждены авторы.
Предложенная екатеринбургскими специалистами теоретическая разработка выводит на новый уровень исследование линий и поверхностей точек ван Хова, что важно для понимания природы топологических особенностей в свойствах твердых тел. Эти фундаментальные результаты важны для конкретных квантовых вычислений электронной структуры.