Московские физики ведут исследования в области квантовой информатики, в частности, разрабатывают новые способы моделирования квантовых систем с использованием методов томографии. Это позволит постичь квантовую природу в динамических системах и избежать помех в квантовых измерениях.
В московском Физико-технологическом институте РАН (ныне ФТИАН им. К. А. Валиева РАН, г. Москва) еще в 90-e годы предыдущего столетия начали закладываться фундаментальные физические основы квантовых информационных технологий.
Для обеспечения оценки качества и эффективности квантовых информационных систем потребовалась методология контроля квантовых состояний и процессов. Так, в институте была создана методология оценивания качества и эффективности квантовых информационных технологий, основанная на анализе полноты, адекватности и точности реализации квантовых вентилей.
Продолжая научные традиции советской физическо-технологической школы академика К. А. Валиева, доктор физ.-мат. наук Ю. И. Богданов совместно с единомышленниками занимается разработкой инновационных методов и алгоритмов анализа качества квантовых операций для задач создания элементной базы квантовых компьютеров.
Большая работа проделана для анализа квантовых операций, в частности, представлены методы описания влияния квантовых шумов на качество элементной базы квантовых компьютеров и проведен анализ квантовой запутанности, являющейся главным звеном в изучении квантовых информационных технологий.
Сотрудники Физико-технологического института идут в направлении внедрения методов анализа в области оптимизации квантовых информационных технологий путем аналитических, численных и экспериментальных исследований. Но здесь важно учитывать, так называемую, декогерентизацию квантовых состояний, обусловленную квантовыми шумами. Это одна из актуальных проблем, встающих на пути создания полномасштабных квантовых компьютеров.
Юрий Иванович Богданов – доктор физ.-мат. наук, главный научный сотрудник, руководитель лаборатории физики квантовых компьютеров Физико-технологического института им. К.А. Валиева РАН (сокр. ФТИАН им. К.А. Валиева РАН) (г. Москва). Профессор Национального исследовательского университета “Московский институт электронной техники” МИЭТ с 2005 г. и профессор Национального исследовательского ядерного университета МИФИ с 2012 г. Достижения: предложил и развил новый метод томографии квантовых состояний и процессов. Впервые сформулировал точные количественные критерии оценки квантовых операций по конечному числу представителей статистического ансамбля, а также развил и применил практически методы и алгоритмы, обеспечивающие достижение прецизионной точности, близкой к фундаментальному пределу. Автор более 200 научных трудов
Руководитель исследования по изучению процессов в квантово-информационных технологиях Юрий Иванович Богданов – специалист в области квантовой информатики и квантовой физики, доктор физ.-мат. наук, главный научный сотрудник, руководитель лаборатории физики квантовых компьютеров Физико-технологического института им. К.А. Валиева РАН (ФТИАН им. К.А. Валиева РАН), а также участники его рабочей группы – сотрудники института и коллеги из Национального исследовательского университета «Московский институт электронной техники»» (НИУ МИЭТ) – подробно рассказали, каковы важные составляющие квантовой информации они изучали и каких эффективных результатов уже достигли. Например, что оценивает квантовая томография, как возникают квантовые шумы и какую роль они играют в элементной базе квантовых компьютеров; каким образом можно преодолеть спам-ошибку в квантовых процессах и что есть «квантовый вампир».
Лаборатория физики квантовых компьютеров создана К.А. Валиевым в 1998 году и является исторически первой лабораторией России в этой области. Последователи наследия академика Валиева продолжают развивать идеи в Физико-технологическом институте РАН, носящем теперь его имя.
Коллектив лаборатории, возглавляемой доктором физ.-мат. наук Юрием Богдановым, сегодня активно занимается моделированием квантовых систем, тесно связанным с корневым подходом в квантовых измерениях.
Так, моделирование квантовых систем методом томографии помогает отслеживать качество элементной базы квантовых компьютеров. Он основан, по словам Юрия Богданова, «на генерации данных методом Монте-Карло и их целенаправленной томографии в направлении минимума энергии. При этом численная процедура решения задачи базируется на оптимизации целевого функционала, обеспечивающего компромисс между максимизацией статистической функцией правдоподобия и минимизацией энергии. Разработанный метод оказался свободен от сложных и плохо обусловленных многомерных вычислительных процедур. Предложенный подход может быть применен для расчета волновых функций и энергий основного и возбужденных стационарных состояний сложных квантовых систем».
«Квантовая томография состояний – это метод восстановления амплитуд квантового состояния по результатам серии измерений. Данная процедура необходима при создании полномасштабного квантового вычислительного устройства. На основе полученных томографических результатов можно сделать вывод о качестве обеспечиваемых квантовых операций, провести необходимые корректировки и сформировать требования к аппаратному обеспечению для достижения более высокого качества квантовых вычислений», – продолжает доктор физ.-мат. наук Юрий Богданов.
Надежда Богданова – кандидат физ.-мат. наук, доцент Национального исследовательского университета «Московский институт электронной техники»» (НИУ МИЭТ) (г. Москва)
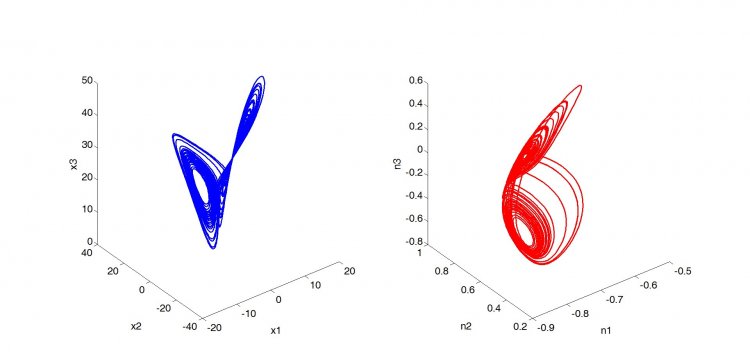
Ответ руководителя лаборатории квантовых компьютеров дополняет доцент НИУ МИЭТ Надежда Богданова: «Важно также отметить, что корневой подход позволяет, с использованием разрабатываемых в настоящее время квантовых симуляторов, обеспечить моделирование широкой группы сложных динамических систем. Нами был разработан общий подход к моделированию классических динамических систем, основанный на их расширении до квантовых состояний. Развитая теория может быть применена к анализу множества (в том числе, и негамильтоновых) диссипативных динамических систем. В качестве примеров мы рассмотрели логистическую модель, осциллятор Ван дер Поля, динамические системы Лоренца, Рёслера (включая Ресслеровский гиперхаос) и Рабиновича-Фабриканта. Важно отметить, что квантовая динамическая система содержит больше информации, чем исходная классическая система. В частности, согласно квантовой механике, мы можем рассматривать не только координатное представление, но и импульсное представление. Известно, что взаимно дополнительные координатное и импульсное представления связаны через фундаментальное соотношение неопределенности Гейзенберга. Сжатие фазового пространства в определенном направлении в координатном представлении указывает на расширение в пространстве импульсов в том же направлении и наоборот. Мы используем это свойство. В частности, чтобы найти показатели неустойчивости Ляпунова в исходном координатном пространстве, мы выполняем более простые вычисления в импульсном пространстве. С фундаментальной точки зрения одновременное рассмотрение взаимодополняющих систем координат и импульсов обеспечивает более глубокое понимание природы хаотического поведения в динамических системах. С вычислительной точки зрения новый формализм служит основой для анализа сложных динамических систем с использованием квантовых симуляторов. На наш взгляд, разработанные методы и алгоритмы, интегрированные в квантовые симуляторы, позволят решить широкий круг задач, имеющих научную и практическую значимость».
«На мой взгляд, в настоящее время методы квантовой информатики должны очень существенно изменить облик общих математических курсов. Так, в последние годы вместо традиционного курса дискретной математики я читаю лекционный курс «Дискретная математика и квантовая информатика», который основан на симбиозе указанных дисциплин», – подчеркнула Надежда Богданова.
Рисунок 1. Представлен аттрактор в системе Лоренца. Слева координатное представление, справа импульсное представление.
Для контроля многофотонных квантовых состояний, базирующегося на глубинных основах квантовой теории, физики разработали модели, опираясь на так называемый корневой подход. Он представляет собой общий метод, основанный на симбиозе методов математической статистики и фундаментальных принципов квантовой теории.
По замечанию Юрия Богданова, этот метод связан «с разработкой и реализацией различных протоколов квантовых измерений и может быть применен не только для контроля многофотонных квантовых состояний, но и для любых других квантовых технологий, включая сверхпроводниковые, оптические, атомные и другие».
Юрий Богданов уточняет, что «математически это сводится к взятию квадратного корня из матрицы плотности (отсюда название метода – корневой подход). Замечательным является тот факт, что совместно с методом максимального правдоподобия корневой подход даёт простое квазилинейное уравнение, решением которого является прямоугольная, в общем случае комплексная матрица, которая по простым правилам матричной алгебры задаёт искомую положительно определённую матрицу плотности системы. Регулируя число столбцов матрицы, задающей «очищенное» состояние, мы можем задавать число независимых компонент статистической смеси и вырабатывать таким образом модель квантового состояния, которая наилучшим образом отражает физическую реальность».
Действие корневого подхода было подтверждено специалистами на практике, в частности, его эффективность была продемонстрирована в ряде экспериментов с оптическими и сверхпроводниковыми квантовыми состояниями.
«Адекватность получаемых моделей подтверждалась соответствующими статистическими тестами и согласием с полученным в наших работах теоретическим распределением точности. Аналогичный подход мы применяем не только для томографии отдельных состояний, но и для томографии квантовых процессов, которые описывают преобразования сразу большой группы различных квантовых состояний. В течении довольно длительного времени нами разрабатывалась программная библиотека для языка MATLAB, которая позволяет осуществлять реконструкцию квантовых состояний посредством корневого подхода и метода максимального правдоподобия», – добавляет кандидат физ-мат. наук, младший научный сотрудник ФТИАН РАН Борис Бантыш.
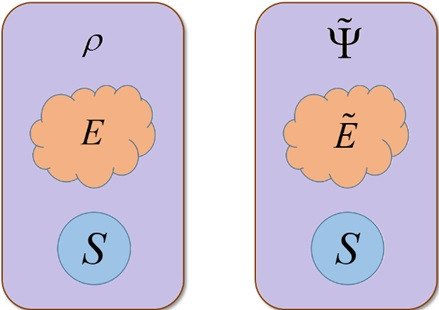
Рисунок 2. Слева – схема реалистичной физической ситуации. Система S, находясь в запутанном состоянии Ψ со своим окружением E при усреднении по степеням свободы окружения, описывается некоторой матрицей плотности ρ. Процедура очищения (справа) состоит в том, чтобы подобрать такое возможное запутанное состояние системы и её гипотетического окружения , чтобы усреднение по степеням свободы давало бы ту же матрицу плотности ρ для системы S. В процессе томографии с использованием корневого подхода осуществляется реконструкция волновой функции .
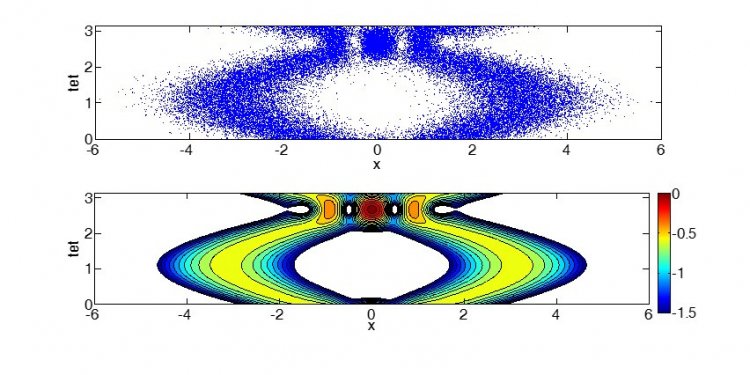
Пример того, как корневой подход позволил обеспечить разработку методов прецизионных многопараметрических квантовых состояний, в том числе и таких экзотических, как состояние кота Шредингера.
Рисунок 3. Восстановление состояния кота Шредингера. Сравнение квадратурных данных (вверху) с результатами статистического восстановления (внизу).
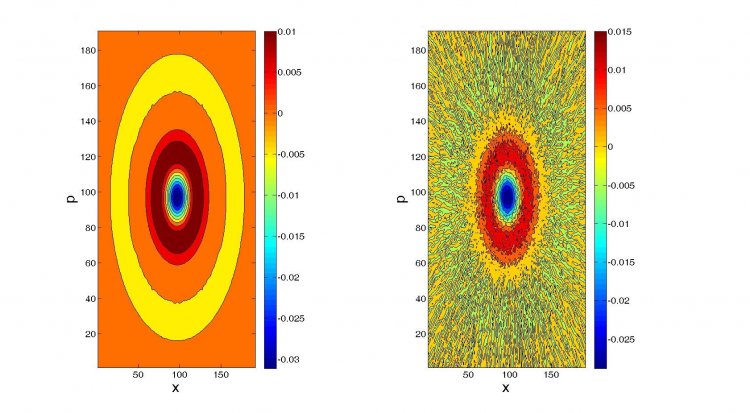
Здесь представлено сравнение точности измерения квантового состояния, которая может быть достигнута посредством развитой корневой оценки (root estimator) с точностью, которую обеспечивает стандартная технология (обратное преобразование Радона, основанное на попытке перенесения методов классической томографии в квантовую область). Реконструировалась так называемая функция Вигнера для однофотонного состояния. Стандартный метод (рисунок справа) обеспечивает низкую точность восстановления квантового состояния (всего 92,4%). В то же время, корневая оценка (root estimator) обеспечивает, точность, которая измеряется шестью девятками (99,99994%).
Рисунок 4. Сравнение точности измерения квантового состояния, которая может быть достигнута посредством корневой оценки (root estimator - рисунок слева) с точностью, которую обеспечивает стандартная технология (обратное преобразование Радона - рисунок справа).
Иллюстрации предоставили Юрий Богданов (ФТИАН им. К. А. Валиева РАН) и Грант Авосопянц (НИУ МИЭТ)
Важно учитывать фотонное тепловое состояние света, то есть самое распространенное состояние света в природе, исследование которого тесно связано с развитием квантовой физики.
Кандидат физ.-мат. наук, старший научный сотрудник ФТИАН РАН Константин Катамадзе ввел в курс становления неклассической физики, популярно объясняя важность квантовых явлений для науки и технологий:
«Собственно, само рождение квантовой физики обычно принято связывать с докладом Макса Планка «К теории распределения энергии излучения нормального спектра», сделанным 14 декабря 1900 года на заседании Немецкого физического общества. В своем докладе Планк смог описать форму спектра, так называемого абсолютно черного тела, используя, как ему тогда казалось, техническое предположение о том, что энергия света изменяется дискретно. К слову, ещё за 28 лет до Планка, представления о квантованном характере энергии в методических целях использовал Людвиг Больцман в своей знаменитой работе 1872 г., в которой им была сформулирована известная H-теорема, обеспечивающая статистическую интерпретацию второго начала термодинамики. Замечательно, что концепция квантов, которая для Больцмана и Планка была не более, чем методическим или техническим приемом, оказалась путеводной звездой развития всей физики 20-го столетия, ровно, как и основой квантовых технологий 21-го столетия.
Позже, в 1956 г. Роберт Хэнбери Браун и Ричард Твисс экспериментально продемонстрировали еще одно удивительное свойство теплового света – так называемую группировку фотонов. Вероятность обнаружить фотон одновременно с другим фотоном оказалась в два раза выше, чем в произвольный момент времени. Это свойство называется корреляцией. Но такие корреляции можно объяснить и, не прибегая к квантовой физике. В то же время, существуют другие, более сложные состояния света, которые демонстрируют квантовые корреляции, лежащие за рамками классической физики, и являющиеся основой для многих приложений, например, для квантовых вычислений и квантовой метрологии.
Для того чтобы определить преимущество использования квантовых состояний света, ученые повторяют эксперименты с классически коррелированными тепловыми состояниями. Например, недавно мы показали, что эффект квантового вампира, который изначально был продемонстрирован на неклассических однофотонных и двухфотонных состояниях света, можно осуществить и с тепловыми состояниями».
Что же такое эффект «квантового вампира» и каким образом он получается – Константин Катамадзе раскрыл далее со своим коллегой аспирантом НИУ МИЭТ Грантом Авосопянцем. Физики уточнили, что имеют в виду условные состояния, при которых свет делится на два или более каналов. При этом регистрация фотона в отдельном канале происходит только в том случае, если одновременно аналогичные фотоны регистрируются и во всех остальных каналах, что обеспечивается использованием электронной схемы совпадений.
«Эффект квантового вампира состоит в том, что если для таких условных состояний в одном из каналов осуществить операцию уничтожения фотона (фактически отщепить один фотон с помощью делителя пучка), то при этом изменится интенсивность всего пучка в целом, независимо от того, в какой части пучка был обнаружен фотон. Фактически, это означает, что операция уничтожения (отщепления) фотона не отбрасывает тени – отсюда и название эффекта. Изначально, рассматриваемый эффект был продемонстрирован лишь для неклассических однофотонных состояний света, но нам удалось показать, что он также работает и для пучков от теплового источника, например, от лампы накаливания, или от лазерного излучения, пропущенного через вращающийся матовый диск. Более того, нам удалось в явном виде показать, что, удалив фотон в некоторой области широкого пучка, мы действительно не наблюдаем тени!
«Условные квантовые состояния, о которых мы говорим, обладают важными и интересными свойствами, которые подчас кажутся парадоксальными. Так, отщепляя фотоны, фактически уменьшая их число, мы можем приготавливать такие условные состояния света, которые имеют более высокую энергию по сравнению с исходным тепловым состоянием. Парадокс здесь, конечно же, мнимый. Дело в том, что в условных состояниях света участвуют не все представители исходного квантового статистического ансамбля, а только те, в которых было отщеплено заданное число фотонов. Очевидно, что фотоны отщепляются, в первую очередь, в тех случаях, когда их много в исходном состоянии. Понятно, что при такой селекции, остаются, в основном, представители, содержащие большое число фотонов,
– сказали ученые московской лаборатории и подчеркнули также –
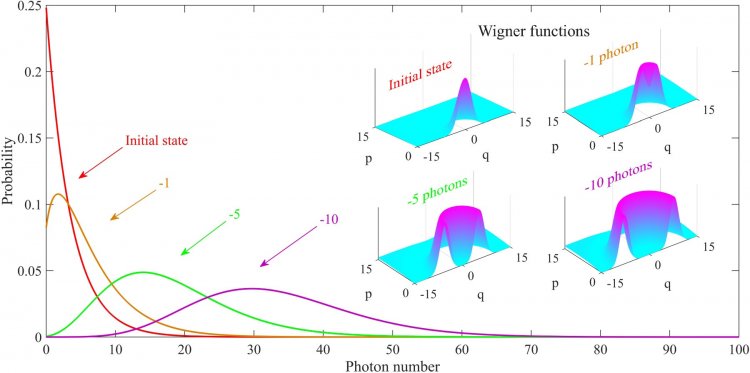
Специально для такого рода задач нами была разработана детальная теоретическая модель, которая хорошо объясняла экспериментальные данные. В этой области исследований нами совместно с физиками из МГУ был выполнен довольно широкий цикл работ. В частности, были приготовлены и детально проанализированы тепловые состояния, из которых было отщеплено от 1 до 10 фотонов (см. Рисунок 5)».
Рисунок 5. Распределение числа фотонов, а также функции Вигнера для исходного теплового состояния, а также для тепловых состояний, состояний, из которых отщеплено соответственно 1,5 и 10 фотонов.
Для того чтобы избежать ошибок при квантовых измерениях эксперты разработали такой метод деконволюции шума, который оптимально приспособлен для применений в квантовых технологиях. В чем его суть и какого рода квантовые ошибки он учитывает? – помог понять Борис Бантыш.
Стандартные методы деконволюции шума давно используются в задачах анализа сигналов и изображений. Классическим примером свёртки является расфокусировка изображения, когда каждая точка изображения превращаются в гауссову функцию (ядро свёртки), хвосты которой «залезают» на соседние точки. В результате происходит потеря чёткости всего изображения. Нечто похожее происходит и при измерении произвольных квантовых состояний.
«Деконволюция (или обратная свёртка) представляет собой попытку восстановить идеальный сигнал по зашумлённому. Такая задача, однако, зачастую является плохо обусловленной и неустойчивой к статистическим флуктуациям. Статистика, получаемая в результате деконволюции шума, как правило, не способна адекватно описывать какое-либо квантовое состояние, – разъяснил младший научный сотрудник ФТИАН РАН Борис Бантыш –
Развиваемый нами подход нечётких квантовых измерений, позволяющий радикально улучшить точность результатов, переносит задачу учёта декогеренции на процедуру реконструкции, используя при этом исходные зашумлённые данные, полученные в эксперименте. Вместо того, чтобы корректировать результаты измерений, мы корректируем саму модель измерений, которая привела к таким результатам. Математически это сводится к замене модели идеальных проекционных измерений на модель POVM-измерений общего вида (POVM – Positive Operator Valued Measure). Квантовая томография с использованием концепции нечётких измерений устойчива к статистическим флуктуациям, а применение её к развитой нами теории точности позволяет количественно оценивать объём информации, потерянной из-за неидеальностей измерительной процедуры».
Основываясь на квантовых измерениях специалисты занимаются разработкой протоколов измерения многокубитовых перепутанных состояний. На базе анализа полной информации можно теоретически оценивать достижимую точность томографии различных состояний ещё до проведения измерений.
Так в последней работе ученые предложили такие квантовые протоколы измерений, основанные на преобразовании Лоренца и выявили четырехмерное псевдовращение квантового состояния для точных измерений в задачах томографии («The concept of weak measurements and the super-efficiency of quantum tomography» в International Conference on Micro- and Nano-Electronics 2018, Proc. of SPIE, Vol. 11022, 110222O, 2019).
Здесь речь идет о преобразованиях Лоренца, вполне аналогичных тем, которые рассматриваются в специальной теории относительности.
Как сообщили доцент Надежда Богданова и инженер, аспирант НИУ МИЭТ Юрий Кузнецов, в этой работе ученые рассмотрели «связь между процедурой квантовых измерений с использованием формализма преобразований Лоренца и задачей контроля квантовой системы посредством её слабого возмущения. В простейшем случае однокубитовых состояний оказывается, что помимо трехмерных вращений на сфере Блоха можно рассматривать четырехмерные псевдовращения, подобные преобразованиям Лоренца, характерным для специальной теории относительности. Наряду с системами с одним кубитом, теория преобразований Лоренца может быть применена и к системам со многими кубитами.
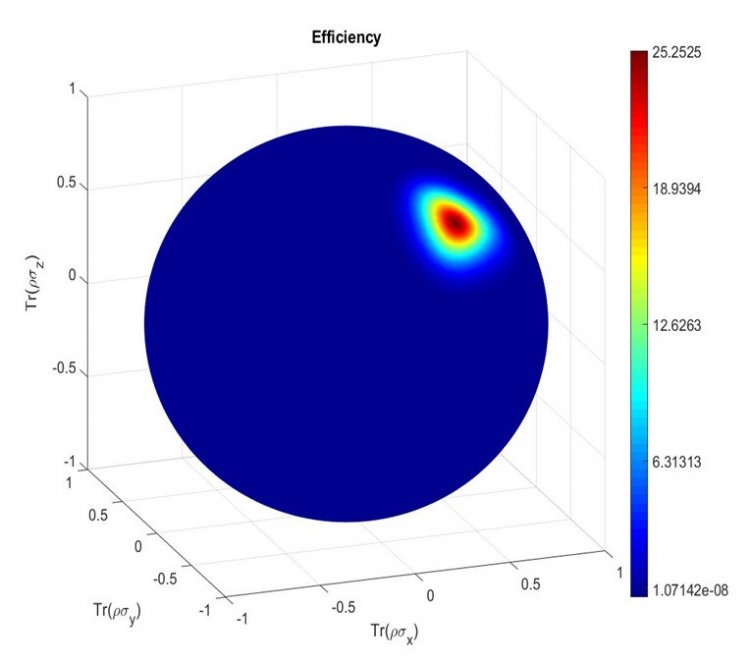
Оказывается, что протоколы квантовых измерений, основанные на преобразованиях Лоренца, не сводятся к стандартному разложению единицы (POVM) и могут быть сверхэффективными, обеспечивая более высокую точность, чем любые стандартные POVM-протоколы. В то же время, посредством введения дополнительного оператора измерений протоколы Лоренца могут быть дополнены до стандартных POVM. В случае состояний, которые обладают малой засоренностью и близки к чистым, дополнительный оператор измерения соответствует слабому возмущению состояния, в то время, как операторы измерения исходного протокола Лоренца задают сильные возмущения (таким образом, обратная связь обеспечивает реальный эффективный контроль квантовой системы, внося при этом только слабые возмущения в квантовое состояние). Результаты проведенного исследования, на наш взгляд, имеют существенное значение для разработки методов контроля квантовых информационных технологий».
Рисунок 6. Распределение на сфере Блоха эффективности для протокола Лоренца. Максимальная и минимальная эффективность, соответственно, есть: , . Здесь демонстрируется локальная природа сверхэффективности. Рассматриваемый протокол Лоренца обеспечивает экстремально высокую точность томографии только в весьма малой области вблизи искомого состояния. При этом для абсолютного большинства состояний на сфере Блоха точность оказывается весьма низкой. Так минимальная точность томографии на сфере Блоха меньше максимальной более чем в миллион раз. Для настройки протокола на нужное состояние следует использовать адаптивную процедуру, когда измерения начинаются с какого-либо стандартного протокола и приближаются к рассматриваемому протоколу Лоренца по мере увеличения объема выборки.
Недавние исследования, проводимые рабочей группой лаборатории квантовых компьютеров, велись и по другим направлениям.
Например, физики применили нейронные сети к квантовой томографии с учетом влияния шумов («Machine learning methods in quantum computing theory» в International Conference on Micro- and Nano-Electronics 2018, //Proc. of SPIE Vol. 11022, 110222S, 2019).
Каким же образом нейронные сети можно использовать для изучения квантовых шумов?
Объясняет младший научный сотрудник, аспирант НИУ МИЭТ Дмитрий Фастовец: «Нейронные сети и наука машинного обучения в целом находят широкое применение в самых различных научных и практических задачах. Не являются исключением и квантовые вычисления. Концепция обучения модели на известных данных хорошо ложится на задачу квантовой томографии: предсказать амплитуды квантового состояния на основе результатов измерений в различных базисах. Естественно, подход, связанный с использованием нейронных сетей уступает классическим методам томографии, основанных на использовании метода максимального правдоподобия. Однако использование искусственных нейронных сетей позволяет решать более широкие задачи. Например, восстановление квантового состояния по зашумленным данным, или подбор оптимальных параметров модели, результаты измерений которой совпадали бы с реальными измерениями. Оба этих подхода успешно опробованы нами на облачном квантовом процессоре IBM».
В другой работе ученые предложили метод реконструкции, который мог бы эффективно рассмотреть спам-ошибку в квантовых процессах– “identity gate” (об этом в статье «High-fidelity quantum tomography with imperfect measurements» в издании International Conference on Micro- and Nano-Electronics 2018, //Proc. of SPIE Vol. 11022, 110222N, 2019).
По словам одного из авторов исследования, Бориса Бантыша, «ошибки приготовления и измерения (SPAM – State Preparation And Measurement – errors) являются одной из весьма существенных проблем, ограничивающих точность томографии квантовых процессов. Для определения параметров неизвестного квантового процесса необходимо пропускать через него различные квантовые состояния, после чего производить над ними взаимно-дополнительные измерения. Далее по результатам измерений производится реконструкция параметров квантового процесса, для чего мы используем корневой подход и метод максимального правдоподобия».
Но в экспериментальных исследованиях часто игнорируют ошибки, что сказывается на оценке параметров квантового процесса и на точности реконструкции. В связи с этим специалисты из МИЭТ и ФТИАН РАН предложили метод экспериментального определения SPAM-ошибок путём томографии идеального единичного преобразования.
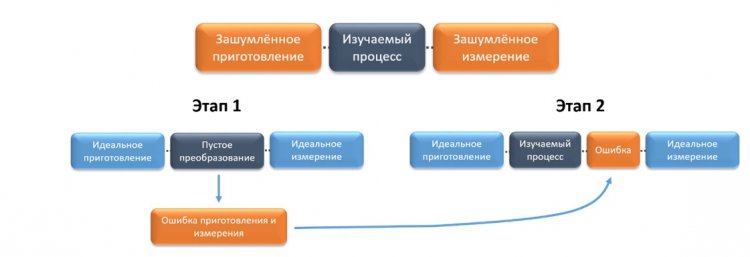
«Такое преобразование всегда может быть реализовано на любой физической платформе, поскольку оно представляет собой просто отсутствие какого-либо преобразования («empty gate» – пустое преобразование). Иными словами, после приготовления входного состояния, необходимо сразу произвести его измерение. После проведения полного набора измерений осуществляется реконструкция квантового процесса. В случае отсутствия SPAM-ошибок результатом оказался бы процесс, соответствующий идеальному единичному преобразованию. В действительности же будет получен некоторый квантовый процесс, который аккумулирует в себе часть ошибок приготовления и измерения. Результат томографии пустого преобразования впоследствии используется для коррекции модели измерений на основе подхода нечётких измерений (см. Рисунок 7). В нашей работе мы, используя сверхпроводниковый квантовый процессор IBM, экспериментально показали, что такая двухэтапная томография значительно повышает точность реконструкции одно- и двухкубитовых процессов», – Борис Бантыш пояснил, на чем основан алгоритм отслеживания этого метода.
Рисунок 7. Сверху – блок-схема эксперимента по томографии квантового процесса. Приготовления и измерение зашумлены, структура шума при этом неизвестна. Снизу – двухэтапный подход по решению проблемы наличия SPAM-ошибок. На первом этапе производится томография идеального пустого преобразования в предположении отсутствия SPAM-ошибок. Результат этой томографии используется на втором этапе для коррекции модели идеальных измерений
Для понимания возможностей квантового мира и объяснения многих его процессов ученым еще предстоит понять философию существования этих мельчайших частиц. Тем временем, московские физики-исследователи и инженеры, опираясь на высокий теоретический аппарат и разработанные методики изучения, оценивают реальные шансы на устранения разного рода ошибок и квантовых шумов в квантовых измерениях и информационных технологиях.
На фото – сотрудники лаборатории физики квантовых компьютеров ФТИАН им. К.А. Валиева РАН
Слева направо: Дмитрий Фастовец (мл. науч. сотр., аспир. НИУ МИЭТ), Юрий Кузнецов (инженер, аспир. НИУ МИЭТ), Борис Бантыш (мл. науч. сотр., к.ф.-м.н.), Игорь Семенихин (стар. науч. сотр., к.ф.-м.н), Юрий Богданов (глав. науч. сотр., зав. лаб, д.ф.-м.н), Андрей Чернявский (стар. науч. сотр., к.ф.-м.н), Константин Катамадзе (стар. науч. сотр., к.ф.-м.н)