Российские ученые построили строгое аналитическое решение канонической задачи дифракции волноводной моды на открытом конце круглого волновода с диэлектрическим заполнением. Этот результат может послужить дальнейшему развитию пучковых методов генерации излучения, а также методов диагностики пучков заряженных частиц и управления их структурой. Исследование выполнено при финансовой поддержке Президентской программы Российского научного фонда (РНФ) и опубликовано в IEEE Transactions on Microwave Theory and Techniques (https://ieeexplore.ieee.org/document/9382413/).
Научная группа. Источник: Сергей Галямин/СПбГУ
Дифракция в простом понимании — это отклонение направления распространения волны от прямолинейного при прохождении мимо какого-либо объекта. Теория дифракции, которая рассматривает это явление более широко и с помощью математических методов, обычно имеет дело с так называемыми каноническими задачами, то есть задачами взаимодействия относительно простых волн со сравнительно простыми геометрическими объектами, такими как, например, бесконечно тонкое ребро, клин, шар, цилиндр и тому подобное. Отдельный класс канонических задач связан с дифракцией волн в резонаторах и на открытом конце волноводов.
Волноводные и резонаторные структуры — одни из ключевых элементов современных ускорителей частиц. В классических ускорителях эти структуры являются чисто вакуумными. Однако в последние годы большое внимание уделяется волноводам и резонаторам с различным диэлектрическим заполнением, так как это открывает перспективы для использования в ускорительной физике эффекта Вавилова-Черенкова. Он возникает при движении заряженной частицы со скоростью, превышающей фазовую скорость распространения волн в среде (в данном случае — в диэлектрике). Излучение расходится конусом от траектории движения частицы, и, поскольку угол при вершине конуса зависит от скорости частицы и скорости света в среде, физики могут определять скорость заряженной частицы и обнаруживать ее в экспериментах.
В интернете можно найти многочисленные фотографии излучения Вавилова-Черенкова в виде голубого свечения. Однако это лишь то, что мы можем видеть глазом. На самом деле эффект Вавилова-Черенкова проявляется в очень широком диапазоне частот электромагнитного спектра, лишь малая часть которого доступна человеческому глазу. В частности, этот эффект имеет место и в диапазонах гига- и терагерцовых частот, которые наиболее интересны для данной работы. В этой связи следует отметить значительные успехи, достигнутые в последнее время в методе кильватерного ускорения заряженных частиц. В этом методе используется излучение Вавилова-Черенкова на гига- или терагерцовых частотах, генерируемое в волноводе с диэлектриком в виде кильватерной волны. Она подобна той, что возникает за идущими по воде кораблями — правда, в данном случае она имеет электромагнитную природу, а роль «корабля» выполняет движущийся сгусток электронов. Так как частота этой волны может попадать в терагерцовый диапазон, физики обсуждают возможность создания на базе таких кильватерных структур генераторов терагерцового излучения. Его уникальные свойства имеют целый ряд перспективных применений, как сугубо прикладных, например, в системах безопасности, так и чисто научных, связанных с исследованиями структуры материи.
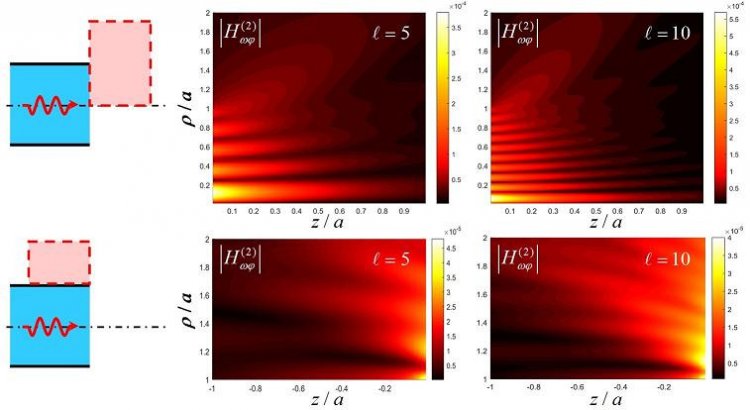
Проникновение волны из волновода с диэлектриком в вакуум и формирование главного
Для развития описанных выше технологий крайне полезно иметь математический метод для строгого решения задачи дифракции электромагнитных волн и задачи дифракции поля движущегося сгустка заряженных частиц на открытом конце круглого волновода со слоем диэлектрика. Другими словами, желательно иметь решение соответствующей канонической задачи. Однако до настоящего момента оно отсутствовало, что, вероятно, связано с математическими сложностями, к которым приводит наличие диэлектрического слоя в волноводе: решение не строится в замкнутом виде, возникают бесконечные линейные или нелинейные системы уравнений. Поэтому ученые кафедры радиофизики Санкт-Петербургского государственного университета (СПбГУ) посвятили свою работу строгому аналитическому решению такой канонической задачи. Свой подход они продемонстрировали на примере сплошного заполнения волновода диэлектриком и возбуждения в виде набегающей волноводной моды. Формально задача состояла в решении одного известного уравнения математической физики, но нужно было наиболее удобным образом выбрать представление для электромагнитного поля в каждой области пространства (волноводные стенки и их продолжения, а также торец волновода являются естественными границами, которые разбивают все пространство на ряд таких областей) и удовлетворить граничным условиям на всех отмеченных границах.
«Мы, конечно, не изобрели этот метод с нуля. В теории дифракции на таких структурах известно достаточно подходов и решено много канонических задач, но как раз нужная в данный момент оказалась нерешенной. Наиболее близко к нашей стоит работа московских физиков Воскресенского и Журава конца 1970-х годов. По большому счету, нам просто удалось понять, как обобщить их подход на случай цилиндрической геометрии, а также мы апробировали полученные результаты современными численными средствами. Разработанный в итоге метод может применяться для решения более сложных и практически значимых задач со слоистым заполнением, при этом возбуждение может быть и в виде свободной волны, и в виде движущегося заряженного сгустка, — говорит Сергей Галямин, руководитель гранта РНФ, кандидат физико-математических наук, доцент кафедры радиофизики СПбГУ. — Кроме того, полученные нами результаты могут применяться для улучшения существующих приближенных подходов и контроля корректности численного моделирования, что особенно важно в случаях, когда моделирование оказывается ресурсозатратным. К решению этих задач мы и планируем приступить в ближайшем будущем».
Информация и фото предоставлены пресс-службой Российского научного фонда