Используя эффект Холла

Екатеринбургские физики в ходе экспериментальных исследований обнаружили квантовый топологический эффект Холла (КТЭХ) в селениде ртути – кандидате в семейство полуметаллов Вейля. Это перспективный магнитотранспортный метод, с помощью которого можно детектировать наличие узлов Вейля в изучаемом материале

Создание принципиально новых электронных устройств требует решения сложных квантовомеханических задач в физике конденсированного состояния. При этом важное значение приобретает изучение транспортных и оптических как поверхностных, так и объемных электронных состояний твердых тел. Не так давно в 2015 году экспериментально были открыты уникальные топологические материалы – полуметаллы Вейля, в которых объемные и поверхностные состояния сосуществуют при одной энергии. Электроны (дырки) в таких состояниях описываются уравнениями Вейля и называются фермионами Вейля. С тех пор поиск и исследование новых представителей семейства полуметаллов Вейля стало приоритетным направлением во многих ведущих мировых исследовательских центрах.

Уральские ученые Института физики металлов в качестве кандидата в семейство полуметаллов Вейля предложили известный бесщелевой полупроводник – селенид ртути. Проведенное ими детальное изучение магнитосопротивления «чистых» монокристаллов HgSe позволило получить важные свидетельства существования электронной фазы полуметалла Вейля в этом материале. Затем физики обратились к исследованию эффекта Холла в квантующем магнитном поле в образце с предельно низкой концентрацией электронов. В итоге уральскими учеными был открыт новый квантовый магнитотранспортный эффект, который они назвали «квантовый топологический эффект Холла», и были сформулированы условия для его наблюдения в полуметалле Вейля.

Александр Трофимович Лончаков – доктор физико-математических наук, ведущий научный сотрудник и руководитель группы топологических полуметаллов лаборатории полупроводников и полуметаллов Института физики металлов имени М.Н. Михеева Уральского отделения РАН (ИФМ УрО РАН) (г. Екатеринбург) – поделился значимыми результатами  трехлетнего исследования и рассказал, что дает изучение эффекта Холла в полупроводнике HgSe для теоретической физики и  в чем состоят ключевые  положения работы.

«Если обратиться к истокам, то эффект Холла, который был открыт в 1879 году американским физиком Эдвардом Холлом, состоит в возникновении на боковых гранях проводника с током, помещенного в поперечное магнитное поле, разности потенциалов, пропорциональной величине тока и индукции магнитного поля. Изучение эффекта Холла как в бесщелевом полупроводнике HgSe, так и в других полупроводниках несомненно способствует развитию теоретических представлений о кинетических свойствах и энергетическом спектре системы. Например, его температурная зависимость может свидетельствовать о наличии или об отсутствии энергетической щели в электронном спектре. Классический эффект Холла активно применяется в качестве одного из основных экспериментальных методов изучения полупроводников. С его помощью можно определять такие важные характеристики полупроводниковой системы, как количество носителей заряда на единицу объема (то есть концентрацию), а также подвижность носителей тока. Пользуясь эффектом Холла, можно отличить квазичастицу с отрицательным зарядом (электрон) от квазичастицы с положительным зарядом (дырки), –

Александр Лончаков провел краткий экскурс истории понятия «эффект Холла» и также пояснил, какова роль этого эффекта в современной физике твердого тела, –

Практически через 100 лет в 1980 году немецким физиком Клаусом фон Клитцингом был открыт другой яркий эффект физики твердого тела, затрагивающий ее глубинные основы, –  целочисленный квантовый эффект Холла (КЭХ). Его суть заключается в том, что в двумерном электронном газе при низких температурах холловское сопротивление ρ_xy перестает быть линейной функцией магнитного поля, как в случае классического эффекта Холла. Вместо этого наблюдается платообразное поведение ρ_xy, причем фиксированная величина плато ρxy является комбинацией целого числа ν (фактора заполнения) и мировых констант (постоянной Планка h и заряда электрона e) и не зависит от типа двумерной структуры, ее размеров, условий эксперимента и т.д.. Соответственно холловская проводимость σ_xy в магнитном поле имеет лестничную структуру c величиной ступеньки (скачка) e²/h».

Где можно наблюдать квантовый эффект Холла и как это способствует пониманию особенностей электронного спектра твердого тела?

«В XXI веке после теоретического предсказания, а затем и экспериментального открытия топологических изоляторов КЭХ наблюдали на двумерных поверхностных дираковских состояниях. В отличие от обычного двумерного электронного газа с квадратичным законом дисперсии в таких системах фактор ν становится полуцелым, что связано с существованием нулевого уровня Ландау в точке Дирака.

Новые перспективы в плане особенностей квантования холловского сопротивления появились после открытия уникальных топологических материалов – полуметаллов Вейля. Эти системы характеризуются наличием в электронном спектре особых точек – узлов Вейля, вблизи которых закон дисперсии является линейным (дираковским). Поэтому иногда полуметалл Вейля называют трехмерным аналогом графена. Например, для полуметаллов Вейля с нарушением симметрии относительно обращения времени (в электронном спектре имеется два узла Вейля с противоположной киральностью) теорией был предсказан квантовый аномальный эффект Холла (КАЭХ).

Для трехмерного электронного газа квант холловской проводимости должен иметь соответствующую размерность (Ом·см)^-1. При этом он теряет свою «двумерную» универсальность e²/h, поскольку становится зависящим от расстояния между узлами Вейля в импульсном пространстве, что и приводит к дополнительному множителю «см^-1». Однако экспериментальному наблюдению плато КАЭХ в открытых к настоящему времени «сложных» полуметаллах Вейля препятствует наличие вклада в эффект Холла от нескольких (как электронных, так и дырочных) вейлевских карманов на поверхности Ферми, наряду с вкладом от тривиальных носителей заряда».

Екатеринбургские физики для своих экспериментальных исследований в качестве полуметалла Вейля выбрали селенид ртути (полупроводник HgSe), потому что основывались прежде всего на его соответствии общим критериям для полуметаллов Вейля. По словам Александра Лончакова, «во-первых, это наличие сильного спин-орбитального взаимодействия, во-вторых, отсутствие в структуре цинковой обманки, в которой кристаллизуется HgSe, центра пространственной инверсии. В дополнение к сказанному имелись как теоретические, так и экспериментальные предпосылки для предположения о существовании в HgSe фазы полуметалла Вейля. С первыми можно связать теорию 2016 г. Руанета с соавторами, из которой вытекает, что HgSe может быть «простым» (идеальным) полуметаллом Вейля с четырьмя парами вейлевских узлов одного вида. Ко вторым прежде всего следует отнести наблюдение в 1997 году методом фотоэлектронной спектроскопии с угловым разрешением (ARPES) двумерных поверхностных электронов, происходивших, по-видимому, от поверхностных Ферми-арок».

Данная работа длилась около трёх лет и носила преимущественно экспериментальный характер, но, по замечанию Лончакова, «с привлечением самых современных теоретических представлений в области физики топологических материалов. Надо сказать, что по ряду позиций наши результаты даже опережают эти представления, что должно стимулировать дальнейшее развитие теории».

В состав рабочей группы топологических полуметаллов лаборатории полупроводников и полуметаллов ИФМ УрО РАН под руководством Александра Лончакова вошли: научный сотрудник Семен Бобин (занимается подготовкой образцов к измерениям, обработкой, анализом и обсуждением полученных экспериментальных данных); младший научный сотрудник Всеволод Дерюшкин (сотрудничал до марта 2020 г.), он занимался подготовкой образцов к измерениям, анализом линейного поперечного магнитосопротивления и квантовых осцилляций в селениде ртути; ведущий научный сотрудник лаборатории углеродных наноматериалов, доктор физико-математических наук Владимир Неверов (специалист в области двумерного квантового эффекта Холла, отвечает за измерение магнитотранспортных свойств при низких температурах на специализированной установке на базе сверхпроводящего соленоида Oxford Instruments).

В ходе исследования еще в 2016 году ученые выдвинули смелую гипотезу о существовании в известном бесщелевом полупроводнике HgSe электронной фазы полуметалла Вейля. Чтобы подтвердить свои предположения, физикам пришлось решить ряд важных и принципиальных задач, которые были связаны с выявлением в HgSe магнитотранспортных признаков, присущих полуметаллам Вейля.

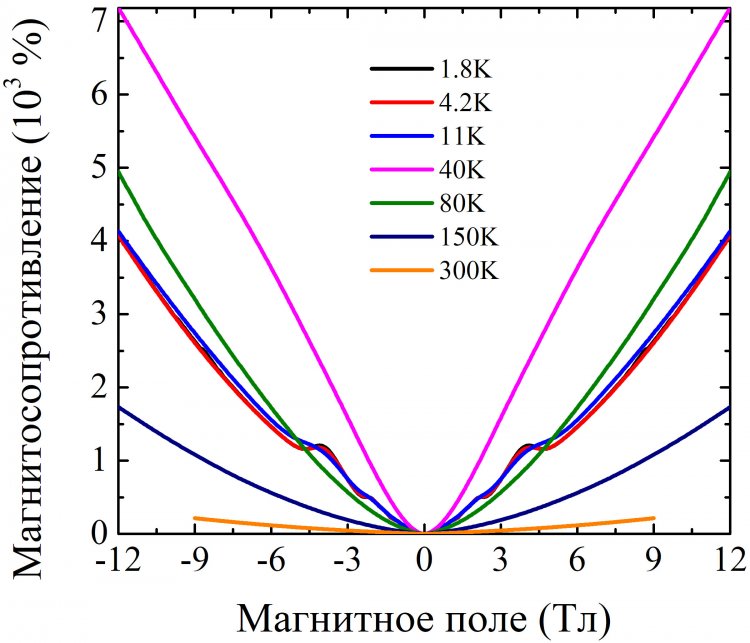
Как комментирует Александр Лончаков, «согласно существующим представлениям фермионы Вейля являются низкоэнергетическими квазичастичными возбуждениями. Поэтому для исследования магнитотранспорта был выбран образец HgSe c достаточно низкой концентрацией электронов – 2.5·10¹⁶ см^-3. Измерение магнитосопротивления проводилось в магнитном поле до 12 Тл в диапазоне температур от 1.8 до 160К. В результате (см. Рис. 1) был выявлен рост поперечного магнитосопротивления (магнитное поле перпендикулярно электрическому току) примерно на 7000% без какой-либо тенденции к насыщению, что характерно для полуметаллов Вейля. При этом продольное магнитосопротивление (магнитное поле параллельно току) в магнитном поле уменьшалось. Этот эффект отрицательного магнитосопротивления мы связали с так называемой «киральной аномалией», присущей только полуметаллам Вейля. Кроме того, мы обнаружили два максимума на температурной зависимости удельного сопротивления в нулевом магнитном поле. Эту особенность также можно объяснить с наличием в HgSe помимо тривиальной бесщелевой фазы в центре зоны Бриллюэна полуметаллической вейлевской фазы.

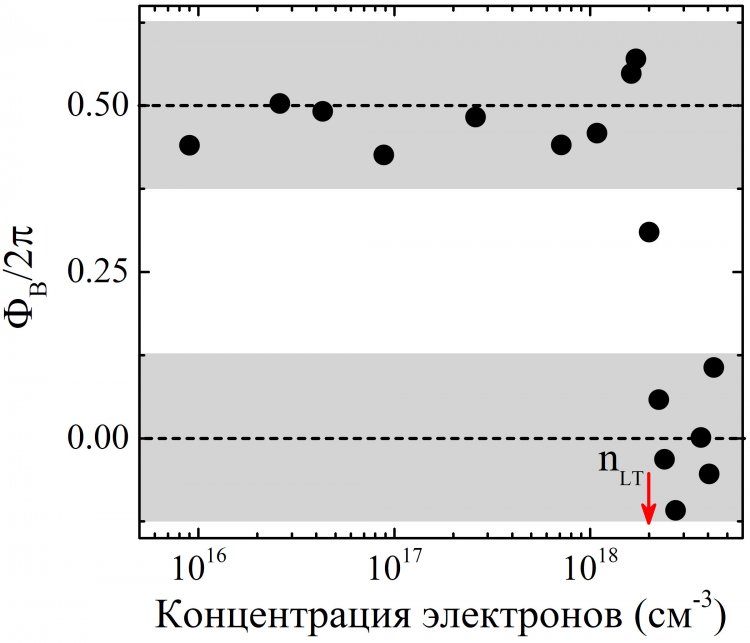
Следующий принципиальный результат – обнаружение нами скачка фазы Берри в HgSe при концентрации электронов приблизительно 2·10¹⁸ см^-3 (см. Рис.2). Он свидетельствует об электронном топологическом переходе Лифшица, что позволило нам оценить один из ключевых параметров для полуметалла Вейля – расстояние в обратном пространстве между узлами Вейля с противоположной киральностью. В HgSe это расстояние оказалось порядка 0.1 обратных ангстрема, что согласуется с данными для других полуметаллов Вейля».

Кроме того, уральские ученые в исследованиях впервые ставили задачу выявления особенностей явлений переноса, связанных с нетривиальной топологией HgSe. Поэтому были выявлены топологические свойства селенида ртути, которые можно считать новыми.

«Нами были обнаружены проявления фазы полуметалла Вейля для параметров спектра (эффективная масса) и рассеяния (подвижность электронов). Мы полагаем, что, изучая селенид ртути, мы имеем дело с «идеальным» (эталонным) полуметаллом Вейля с одним видом узлов Вейля. Поэтому полученные нами результаты могут быть полезными при исследовании более «сложных» полуметаллов Вейля с несколькими видами узлов Вейля, например, относящихся к семейству моноарсенида тантала: TaAs, TaP, NbAs, NbP», –уточняет Александр Лончаков.

Собранные данные, свидетельствующие о нетривиальной топологии HgSe, стали для уральских ученых главной мотивацией для исследования в HgSe эффекта Холла в квантующем магнитном поле с целью обнаружения квантования холловского сопротивления. В конечном итоге, был обнаружен новый поперечный квантовый магнитотранспортный эффект, который заявлен как «квантовый топологический эффект Холла» (КТЭХ).

Каковы условия и характер его формирования и каким методом был вычислен КТЭХ?

Александр Лончаков детально разъяснил: «В качестве объекта исследования был выбран образец с самой низкой для HgSe на тот момент концентрацией электронов 8.8·10¹⁵ см^-3. Исследование, результатом которого явилось открытие принципиально важного для физики конденсированного состояния эффекта, было выполнено в три этапа.

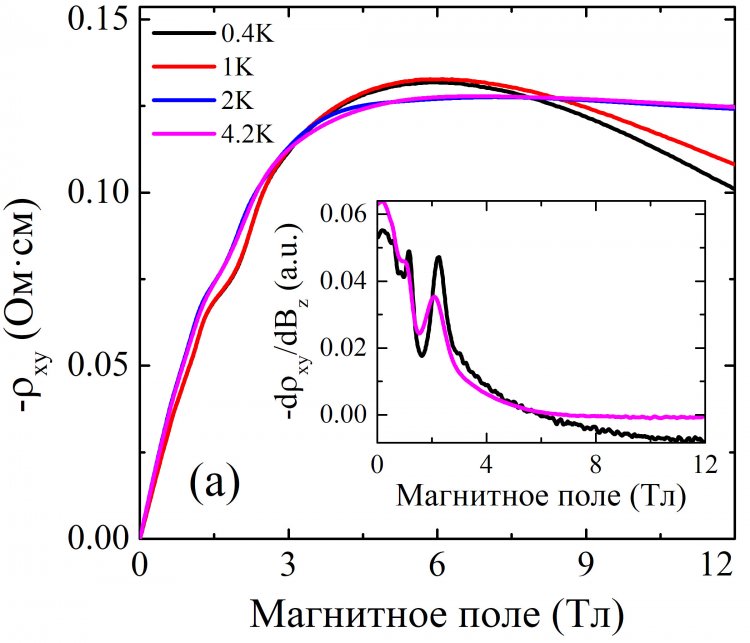
На первом этапе эффект Холла в квантующем магнитном поле был исследован в стандартной (поперечной) холловской конфигурации. В результате на ρ_xy в ультраквантовом пределе выявлено предсказанное теорией протяженное плато (см. Рис.3). Однако предшествующие плато оказались сильно размытыми из-за классического эффекта Холла, связанного с силой Лоренца.

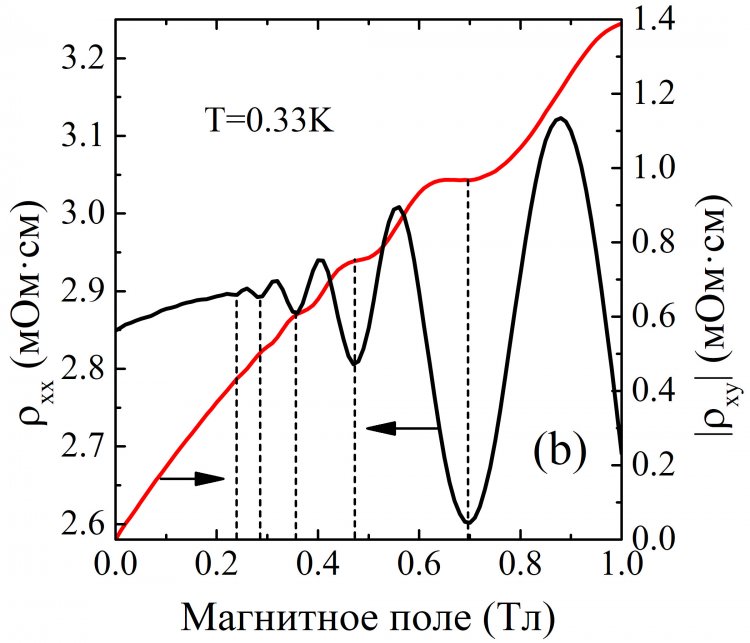
На втором этапе предполагалось избавиться от силы Лоренца, оставив только топологический вклад. Для этого магнитное поле было направлено вдоль электрического тока (продольная конфигурация). Тем самым мы вышли «за флажки» привычных представлений об измерении эффекта Холла. В результате, на холловских контактах образца удалось выявить нечетное по магнитному полю напряжение. Затем феноменологически для этого напряжения было определено «продольное» холловское сопротивление ρ_xy, аналогично обычному (поперечному) холловскому сопротивлению. Как видно (см. Рис.4), такое сопротивление демонстрирует четкое платообразное поведение. При этом показано, что появление плато сопровождается минимумом продольного магнитосопротивления.

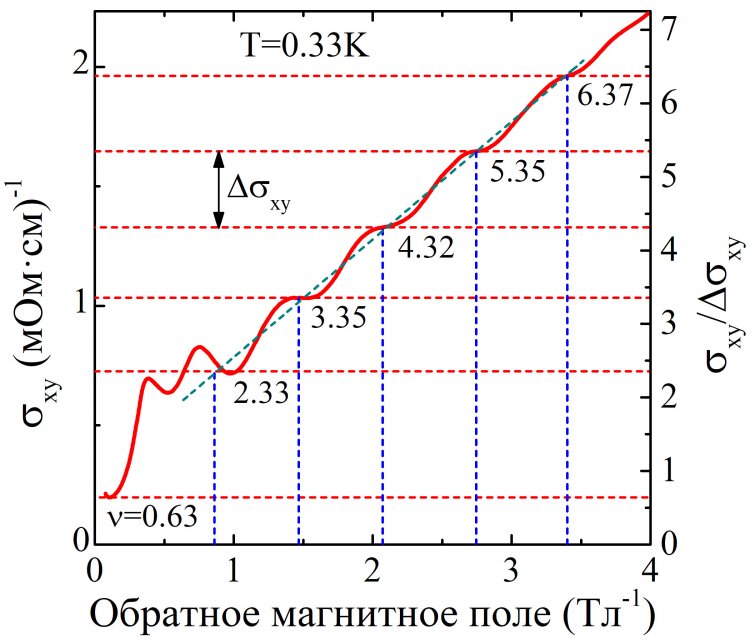
При этом «продольная» холловская проводимость σ_xy в полном соответствии с законами квантования имела лестничную структуру с величиной кванта Δσ_xy = 308 (Ом·см)^-1 (см. Рис.5). Принципиально важно дополнял картину эффекта близкий к полуцелому фактор заполнения ν, подтверждающий наличие в электронном спектре конусов Вейля. Новый поперечный квантовый магнитотранспортный эффект получил название «квантовый топологический эффект Холла» (КТЭХ), поскольку он был обнаружен в полуметалле Вейля – трехмерной системе с нетривиальной кривизной Берри.

На третьем этапе характерная для КТЭХ структура квантования была качественно воспроизведена на образце HgSe с существенно более высокой концентрацией электронов – 2.5·10¹⁷см^-3. Этот важный результат подтверждает топологическую природу явления, связанную с вкладом в проводимость именно фермионов Вейля, а не тривиальных электронов зоны проводимости HgSe».

Как подчеркнул Лончаков, «существующие теоретические представления позволяют ассоциировать открытый в HgSe КТЭХ с полуцелым квантовым спиновым эффектом Холла для полуметаллов Вейля с отсутствующим центром пространственной инверсии. Последний был рассчитан немецкими теоретиками в рамках формализма Кубо с использованием спиновой кривизны Берри. Результаты открытия и исследования КТЭХ были опубликованы в профильных физических журналах (JOURNAL OF PHYSICS: CONDENSED MATTER, 2019 APPLIED PHYSICS LETTERS, 2018) и вызвали заметный интерес у специалистов в области физики конденсированного состояния».

Каковы перспективы использования квантового магнитотранспортного эффекта на основе изученного материала в будущих фундаментальных/прикладных исследованиях?

«Квантование «продольной» холловской проводимости в будущем может стать перспективным магнитотранспортным методом для детектирования узлов Вейля и поверхностных Ферми-арок в изучаемом материале. Полученные результаты открывают новое направление в магнитотранспорте – исследование квантового спинового (квантового аномального) эффекта Холла в топологических полуметаллах», – убежден ведущий научный сотрудник и руководитель группы топологических полуметаллов лаборатории полупроводников и полуметаллов ИФМ Александр Лончаков.

Таким образом, обнаружено новое квантовое явление в вейлевском полуметалле и уточнены условия существования полуметаллической топологической фазы Вейля в селениде ртути, что в итоге позволило рассмотреть и описать квантовый топологический эффект Холла, открывающий  возможности  для его исследования в других  топологических полуметаллах.