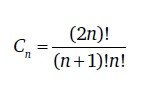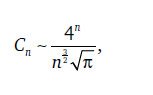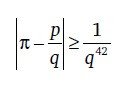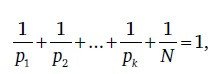1
Неделимая единица
Самое маленькое положительное целое число — это 1. Это неделимая единица арифметики: единственное положительное число, которое невозможно получить путем сложения двух меньших положительных чисел.
Основа концепции числа
С числа 1 мы начинаем счет. Из любого заданного числа можно получить следующее, прибавив к нему единицу:
2 = 1 + 1,
3 = (1 + 1) + 1,
4 = ( (1 + 1) + 1) + 1
и так далее. Скобки говорят о том, какие операции нам следует выполнять первыми. Как правило, скобки опускают, поскольку оказывается, что в данном случае порядок операций не имеет значения, однако лучше всего соблюдать осторожность с самого начала.
Исходя из этих определений и основных законов алгебры, которые при формальном логическом изложении следует сформулировать явным образом, мы можем доказать даже знаменитую теорему «2 + 2 = 4». Доказательство укладывается в одну строчку:
2 + 2 = (1 + 1) + (1 + 1) = ( (1 + 1) + 1) + 1 = 4.
В XX в., когда некоторые математики пытались подвести под математику прочный логический фундамент, они использовали ту же идею, но по техническим причинам начинали с 0 (см. главу 0).
Число 1 выражает важную математическую идею: идею единственности. Математический объект, обладающий каким-то конкретным свойством, является единственным, если этим свойством обладает только он один. К примеру, 2 — это единственное четное простое число. Единственность — важное свойство, поскольку оно позволяет доказать, что какой-то загадочный математический объект на самом деле является тем, о чем мы уже знаем. К примеру, если мы можем доказать, что некое неизвестное положительное число n одновременно четное и простое, то получается, что n должно быть равно 2. Или более сложный пример: додекаэдр — единственный правильный многогранник с пятиугольными гранями (см. главу 5). Поэтому если в каких-то математических выкладках мы встречаем правильный многогранник с пятиугольными гранями, мы сразу, без дальнейших разбирательств, понимаем, что это должен быть додекаэдр. А все остальные свойства додекаэдра мы получаем в придачу в качестве бесплатного приложения.
Таблица умножения на единицу
Никто и никогда не жалуется на то, что ему приходится зубрить таблицу умножения на 1: «Одиножды один — один, одиножды два — два, одиножды три — три…» Любое число при умножении на 1 или при делении на 1 остается неизменным:
n × 1 = n n : 1 = n.
Это единственное число, которое ведет себя подобным образом.
Вследствие этого единица равна собственному квадрату, кубу и всем остальным степеням:
12 = 1 × 1 = 1,
13 = 1 × 1 × 1 = 1,
14 = 1 × 1 × 1 × 1 = 1
и так далее. Единственное другое число, обладающее таким же свойством, это 0.
По этой причине число 1, как правило, опускается в алгебре, если появляется в какой-то формуле в качестве коэффициента. К примеру, вместо 1x2 + 3x + 4 мы пишем просто x2 + + 3x + 4. Единственное другое число, с которым поступают сходным образом, — это 0; с ним происходит нечто еще более радикальное: вместо 0x2 + 3x + 4 мы пишем 3x + 4, просто отбрасывая слагаемое 0x2.
Простое или нет?
Раньше число 1 считалось простым, но сегодня оно таковым не является. Число, разумеется, не изменилось, изменилось определение «простого» числа.
Некоторые числа можно получить путем перемножения двух других чисел: так, 6 = 2 × 3, а 25 = 5 × 5. Такие числа называются составными. Но есть числа, которые невозможно получить таким способом: они называются простыми.
Согласно этому определению, 1 — простое число, и еще 150 лет назад оно таковым и считалось. Но затем оказалось, что удобнее рассматривать 1 как исключительный случай. Сегодня 1 не считается ни простым, ни составным числом, а рассматривается как единица. Я скоро объясню почему, но сначала нам потребуется еще несколько идей.
Последовательность простых чисел начинается как
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47
и выглядит совершенно нерегулярной, если исключить несколько простых закономерностей. Все простые числа, за исключением 2, нечетные, поскольку любое четное число делится на 2. Только 5 может заканчиваться на 5, и никакое простое число не может заканчиваться на 0, поскольку все такие числа делятся на 5.
Любое натуральное число больше 1 можно выразить в виде произведения простых чисел. Это действие называется факторизацией, или разложением на простые множители, а задействованные простые числа называются простыми множителями числа. Более того, разложить число на простые множители можно единственным способом, если не учитывать порядок перемножения простых чисел. К примеру,
60 = 2 × 2 × 3 × 5 = 2 × 3 × 2 × 5 = 5 × 3 × 2 × 2
и так далее, но по существу единственный способ получить 60 состоит в том, чтобы взять первый список простых множителей и расставить их в произвольном порядке. В то же время не существует разложения на простые множители, которое выглядело бы как 60 = 7 × на что-нибудь.
Это свойство называется «единственность разложения на простые множители». Вероятно, оно представляется очевидным, но, если у вас нет ученой степени по математике, я сомневаюсь, чтобы кто-нибудь показывал вам, как оно доказывается. Евклид, который поместил это доказательство в свои «Начала», должно быть, понимал, что оно не является ни очевидным, ни простым, поскольку не спешил и доказывал все достаточно тщательно. Кстати говоря, для некоторых более общих числоподобных систем оно попросту неверно. Но для обычной арифметики это утверждение верно, и это очень эффективное оружие в математическом арсенале.
2 (простое) 3 (простое) 4 = 22 5 (простое) 6 = 2 × 3
7 (простое) 8 = 23 9 = 32 10 = 2 × 5 11 (простое)
12 = 22 × 3 13 (простое) 14 = 2 × 7 15 = 3 × 5 16 = 24
17 (простое) 18 = 2 × 32 19 (простое) 20 = 22 × 5 21 = 3 × 7
22 = 2 × 11 23 (простое) 24 = 23 × 3 25 = 52 26 = 2 × 13
27 = 33 28 = 22 × 7 29 (простое) 30 = 2 × 3 × 5 31 (простое).
Исключительным случаем 1 рассматривается в основном потому, что если считать ее простым числом, то разложение на простые множители перестает быть единственным. К примеру, 6 = 2 × 3 = 1 × 2 × 3 = 1 × 1 × 2 × 3 и так далее. Одно из очевидно неудобных следствий такой договоренности состоит в том, что у 1 нет простых множителей. Однако это число все же является произведением «пустого множества» простых чисел. Иными словами, если перемножить нисколько простых чисел, получится 1. Звучит достаточно безумно, но на самом деле для такого соглашения есть разумные причины. Аналогично, если «перемножить» одно простое число, получится это самое простое число.
Жизнь, вселенная и…
Правда ли, 42 — самое скучное число на свете?
42
Вовсе не скучное
Ну, вот вам и ответ. Как упоминалось в предисловии, это число фигурирует в «Путеводителе по Галактике» Дугласа Адамса, где оно выступает как ответ на «Великий Вопрос Жизни, Вселенной и Всего Остального». Это открытие немедленно поставило новый вопрос: что на самом деле представляет собой великий вопрос жизни, Вселенной и всего остального. Адамс сказал, что он выбрал это число потому, что беглый опрос среди друзей показал, что это совершенно скучное число.
Здесь я хочу защитить число 42 от этого обвинения. Признаю, 42 не сравнится, скажем, с числами 4, или π, или даже 17 по своему математическому значению. Однако нельзя сказать также, что оно совершенно не представляет интереса. Это прямоугольное число, число Каталана и магическая постоянная наименьшего магического куба. Плюс еще кое-что.
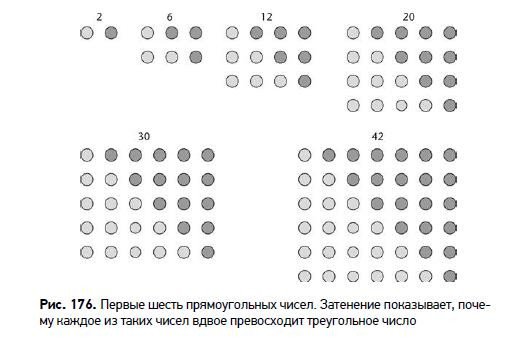
Прямоугольное число
Прямоугольное число представляет собой произведение двух последовательных натуральных чисел. Следовательно, оно имеет форму n (n + 1). Если n = 6, получим 6 × 7 = 42. Поскольку n-е треугольное число равно 1/2 n (n + 1), прямоугольное число вдвое превышает треугольное. Следовательно, оно представляет собой сумму первых n четных чисел. Прямоугольное число точек можно расположить в виде прямоугольника, в котором одна сторона на единицу больше другой.
Рассказывают, что Гауссу в ранней юности задали задачу общего вида
1 + 2 + 3 + 4 + … + 100.
Он сразу же понял, что если ту же сумму записать в обратном порядке слагаемых
100 + 99 + 98 + 97 + … + 1,
то соответствующие пары дадут в сумме 101. Поскольку таких пар 50, полная сумма составит 50 × 101 = 5050. Это прямоугольное число. Однако мы не знаем в точности, какие числа дал классу учитель Гаусса; вероятно, пример был менее красивым. Если это так, то озарение Гаусса было еще более ярким.
Шестое число Каталана
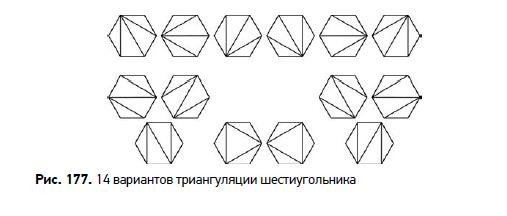
Числа Каталана проявляют себя во многих комбинаторных задачах; они отражают число способов выполнения различных математических операций. Они восходят к Эйлеру, который подсчитал число способов разбиения многоугольника на треугольники путем соединения его вершин. Позже Эжен Каталан открыл связь с алгеброй: сколькими способами можно расставить скобки в некой сумме или произведении. Я скоро перейду к этому, но сначала позвольте представить эти числа.
Первые несколько чисел Каталана Cn для n = 0, 1, 2, … таковы:
1 1 2 5 14 42 132 429 1430 4862.
Существует формула с использованием факториала:
Хорошей аппроксимацией для больших n является
что представляет собой еще один пример того, как π возникает в задаче, которая, казалось бы, не имеет никакого отношения к окружностям или сферам.
Cn — это число различных способов разрезать правильный (n + 2)-угольник на треугольники.
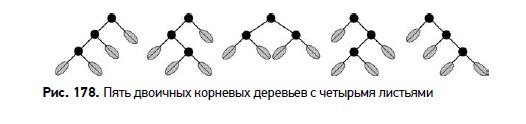
Кроме того, это число корневых двоичных деревьев с n + 1 листьями. Такие деревья получают, начиная с одной точки — корня, из которого затем расходятся две ветви. Каждая ветвь заканчивается либо точкой, либо листом. Из каждой точки, в свою очередь, выходят две ветви.
Если эта идея представляется вам эзотерической, обратите внимание на то, что она непосредственно связана с алгеброй: это число различных способов расставить скобки в произведении, таком как abcd, где существует C3 = 5 вариантов:
( (ab) c) d (a (bc)) d (ab) (cd) a ( (bc) d) a (b (cd)).
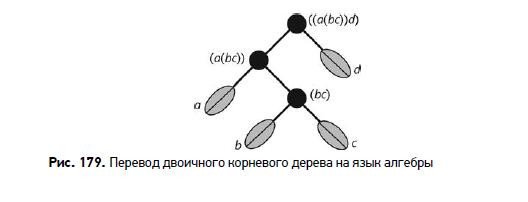
В общем, при n + 1 символах скобок будет Cn. Чтобы увидеть эту связь, напишите символы рядом с листьями дерева и поставьте скобки в соответствии с тем, какие пары сходятся в одной точке. Если говорить подробнее (рис. 179), мы обозначаем листья буквами a, b, c, d слева направо. Двигаясь снизу вверх, пишем (bc) возле точки, в которой сходятся b и c. Затем выше, возле точки, где соединяются a и линия от точки (bc), пишем (a (bc)). Наконец, еще выше, где ко всему этому присоединяется d, пишем ( (a (bc)) d).
Магические кубы
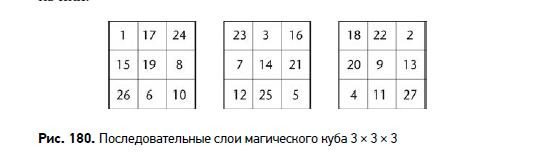
Многие другие комбинаторные задачи также ведут к числам Каталана; вышеприведенные — всего лишь небольшой пример простейших из них. Магические кубы Магическая постоянная магического куба 3 × 3 × 3 равна 42. Такой куб содержит числа от 1 до 27, причем сумма чисел любого ряда, параллельного ребру, или любой диагонали, проходящей через центр куба, одинакова и равна магической постоянной. Сумма всех 27 чисел равна 1 + 2 + … + 27 = 378. Эти числа разбиваются на девять непересекающихся троек, каждая из которых дает в сумме магическую постоянную, так что она должна быть равна 378/9 = 42.
Такие варианты существуют и на рис. 180 показан один из них.
Другие особые свойства
▢ 42 — это число разбиений 10, то есть количество способов записать это число как сумму натуральных чисел в их естественном порядке, например:
1 + 2 + 2 + 5 3 + 3 + 4.
▢ 42 — второе сфеническое число (это числа, представляющие собой произведение трех различных простых чисел). В данном случае 42 = 2 × 3 × 7. Вот первые несколько сфенических чисел:
30 42 66 70 78 102 105 110 114 130.
▢42 — третье пятнадцатиугольное число (это аналог треугольных чисел на базе правильного 15-угольника).
▢42 — суперкратно совершенное число: сумма делителей суммы его делителей (включая 42) вшестеро больше самого числа.
▢ Некоторое время 42 считалось наилучшей известной мерой иррациональности для π, то есть лучшей количественной оценкой того, «насколько π иррационально». Точнее, Курт Малер в 1953 г. доказал, что
для любого рационального p/q . Однако в 2008 г. В. Х. Саликов заменил показатель 42 на 7,60630853, так что число 42 вновь стало скучным в этом отношении.
▢ 42 — третье первичное псевдосовершенное число. Эти числа удовлетворяют условию
где pk — различные простые делители N.
Вот первые несколько первичных псевдосовершенных чисел:
2 6 42 1806 47 058 2 214 502 422 52 495 396 602.
▢ 42 — число n множеств из четырех различных положительных целых чисел a, b, c, d < n, таких что ab – cd, ac – bd и ad – bc делятся на n. Это единственное известное число, обладающее таким свойством; существуют ли другие такие числа, неизвестно.
▢ 42 — наименьшая размерность, для которой гипотеза о колбаске доказана (см. главу 56). Предполагается, однако, что эта гипотеза верна для всех размерностей, больших или равных 5, так что значение числа 42 в этом случае зависит от текущего состояния наших знаний.
Вот видите? Вовсе не скучное!